कुछ फलन और उनके आलेख: Difference between revisions
No edit summary |
(added content) |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
[[Category:गणित]] | [[Category:गणित]] | ||
[[Category:कक्षा-11]] | [[Category:कक्षा-11]] | ||
गणित में, एक समुच्चय X से एक समुच्चय Y तक एक फलन X के प्रत्येक तत्व को Y का ठीक एक तत्व प्रदान करता है। समुच्चय X को फलन का प्रांत(डोमेन) कहा जाता है और समुच्चय Y को फलन का सहप्रांत(कोडोमेन) कहा जाता है। | |||
आईए अब हम कुछ फलन और उनके आलेख के बारे में समझने का प्रयास करते हैं। यह मुख्यतः 7 प्रकार के होते हैं जो की निम्नलिखित हैं: | |||
# तत्समक फलन | |||
# अचर फलन | |||
# बहुपद फलन या बहुपदीय फलन | |||
# परिमेय फलन | |||
# मापांक फलन | |||
# चिह्न फलन | |||
# महत्तम पूर्णांक फलन | |||
== तत्समक फलन == | |||
मान लीजिए <math>R</math> वास्तविक संख्याओं का समुच्चय है। <math>y=f(x)</math>, प्रत्येक <math>x\in R</math> द्वारा परिभाषित वास्तविक मान [[फलन]] <math>f:R\rightarrow R</math> है। इस प्रकार के फलन को तत्समक फलन कहते हैं। यहाँ पर <math>f</math> के प्रांत तथा परिसर <math>R</math> हैं। इसका आलेख एक सरल रेखा होता है(चित्र-1)। यह रेखा मूल बिंदु से हो कर जाती है। | |||
[[File:फलन f(x)=3.jpg|thumb|चित्र-2 f(x)=3]] | [[File:फलन f(x)=3.jpg|thumb|चित्र-2 f(x)=3]] | ||
== अचर फलन == | |||
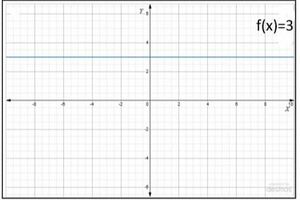
<math>y=f(x)=c</math> जहाँ <math>c</math> एक अचर है और प्रत्येक <math>x\in R</math> द्वारा परिभाषित एक वास्तविक मान फलन <math>f:R\rightarrow R</math> है। यहाँ पर <math>f</math> का प्रांत <math>R</math> है और उसका परिसर <math>\{c\}</math> है। <math>f</math> का आलेख <math>x</math>- अक्ष के समांतर एक [[रेखा]] है, उदाहरण के लिए यदि <math>f(x)=3</math> प्रत्येक <math>x\in R</math> है, तो इसका आलेख (चित्र- 2) में दर्शाई रेखा है। | |||
== बहुपद फलन या बहुपदीय फलन == | |||
फलन <math>f:R\rightarrow R</math>, एक बहुपदीय फलन कहलाता है, यदि <math>R</math> के प्रत्येक <math>x</math> के लिए, <math>y=f(x)=a_0+a_1x+a_2x^2+....+a_nx^n</math>, जहाँ ”<math>n</math>" एक ऋणेतर [[पूर्णांक]] है तथा <math>a_0,a_1,a_2,.....a_n\in R</math> । | |||
<math>f(x)=x^3-x^2+2 </math>, और <math> g(x)=x^4+\sqrt{2}x</math>, द्वारा परिभाषित फलन एक बहुपदीय फलन है जब कि <math>h(x)=x^\frac{2}{3}+2x</math> द्वारा परिभाषित फलन <math>h</math>, बहुपदीय फलन नहीं है। | <math>f(x)=x^3-x^2+2 </math>, और <math> g(x)=x^4+\sqrt{2}x</math>, द्वारा परिभाषित फलन एक बहुपदीय फलन है जब कि <math>h(x)=x^\frac{2}{3}+2x</math> द्वारा परिभाषित फलन <math>h</math>, बहुपदीय फलन नहीं है। | ||
== परिमेय फलन == | |||
<math>\frac{f(x)}{g(x)}</math> के प्रकार के फलन जहाँ <math>f(x)</math> तथा <math>g(x)</math> | |||
एक प्रांत में, <math>x</math> के परिभाषित बहुपदीय फलन हैं, जिसमें <math>g(x)\neq 0</math> परिमेय फलन कहलाते हैं। | एक प्रांत में, <math>x</math> के परिभाषित बहुपदीय फलन हैं, जिसमें <math>g(x)\neq 0</math> परिमेय फलन कहलाते हैं। | ||
| Line 48: | Line 63: | ||
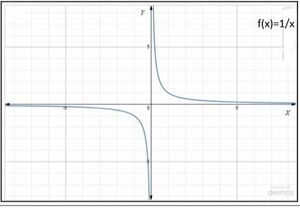
इसका प्रांत, शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं तथा इसका परिसर भी शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं। <math>f</math> का आलेख चित्र-3 में प्रदर्शित है। | इसका प्रांत, शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं तथा इसका परिसर भी शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं। <math>f</math> का आलेख चित्र-3 में प्रदर्शित है। | ||
== मापांक फलन == | |||
[[File:F(x)=IxI.jpg|thumb|चित्र-4 f(x)=IxI]] | |||
<math>f(x)=\left\vert x \right\vert</math> प्रत्येक <math>x\in R</math> द्वारा परिभाषित फलन <math>f:R\rightarrow R</math>, मापांक फलन कहलाता है। <math>x</math> के प्रत्येक ऋणेत्तर मान के लिए <math>f(x)</math>, <math>x</math> के समान होता है। परंतु <math>x</math> के ऋण मानों के लिए, <math>f(x)</math> का मान <math>x</math> के मान के ऋण के बराबर होता है,अर्थात् | |||
<math>f(x)=\begin{cases}x,x\geq 0 \\ -x,x<0 \end{cases}</math> | |||
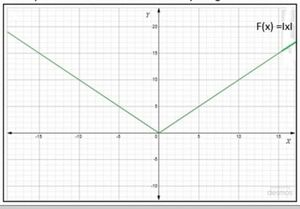
मापांक फलन का आलेख चित्र-4 में दिया है । मापांक फलन को निरपेक्ष मान फलन भी कहते हैं। | |||
== चिह्न फलन == | |||
[[File:F(x)=IxIbyx.jpg|thumb|चित्र-5 f(x)=IxI/x]] | |||
प्रत्येक <math>x\in R</math>, के लिए | |||
<math>1</math>, यदि <math>x>0</math> | |||
x | <math>f(x)=0 </math>, यदि <math>x=0</math> | ||
<math>-1</math>, यदि <math>x<0</math> | |||
f | द्वारा परिभाषित फलन <math>f:R\rightarrow R</math> चिह्न फलन कहलाता है। चिह्न फलन का प्रांत <math>R</math> है। परिसर समुच्चय <math>\{-1,0,1\}</math> है। | ||
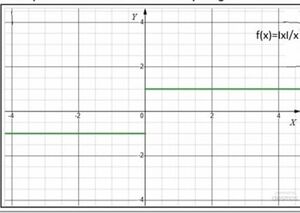
चित्र-5 में चिह्न फलन का आलेख दर्शाया गया है। | |||
[x] = | == महत्तम पूर्णांक फलन == | ||
[[File:1f(x)=IxI.jpg|thumb|चित्र-6 f(x)=IxI]] | |||
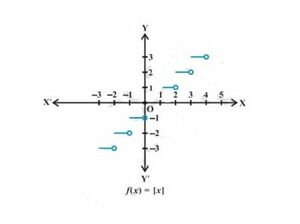
<math>f(x)=[x],x\in R</math> द्वारा परिभाषित फलन <math>f:R\rightarrow R</math> , <math>x</math> से कम या <math>x</math> के बराबर महत्तम पूर्णांक का मान ग्रहण (धारण) करता है ऐसा फलन '''महत्तम पूर्णांक फलन''' कहलाता है। | |||
<math>[x]</math>, की परिभाषा से हम देख सकते हैं कि | |||
[x] = | <math>[x]=-1 </math> यदि <math> -1\leq x<0</math> | ||
<math>[x]=0</math> यदि <math> 0\leq x<1</math> | |||
[x] = | <math>[x]=1 </math> यदि <math> 1\leq x<2</math> | ||
2 यदि | <math>[x]=2 </math> यदि <math> 2\leq x<3</math> इत्यदि | ||
इस फलन का आलेख | इस फलन का आलेख चित्र-6 में दर्शाया गया है। | ||
[[Category:संबंध और फलन]][[Category:कक्षा-11]][[Category:गणित]][[Category:गणित]] | [[Category:संबंध और फलन]][[Category:कक्षा-11]][[Category:गणित]][[Category:गणित]] | ||
Latest revision as of 06:31, 8 November 2024
गणित में, एक समुच्चय X से एक समुच्चय Y तक एक फलन X के प्रत्येक तत्व को Y का ठीक एक तत्व प्रदान करता है। समुच्चय X को फलन का प्रांत(डोमेन) कहा जाता है और समुच्चय Y को फलन का सहप्रांत(कोडोमेन) कहा जाता है।
आईए अब हम कुछ फलन और उनके आलेख के बारे में समझने का प्रयास करते हैं। यह मुख्यतः 7 प्रकार के होते हैं जो की निम्नलिखित हैं:
- तत्समक फलन
- अचर फलन
- बहुपद फलन या बहुपदीय फलन
- परिमेय फलन
- मापांक फलन
- चिह्न फलन
- महत्तम पूर्णांक फलन
तत्समक फलन
मान लीजिए वास्तविक संख्याओं का समुच्चय है। , प्रत्येक द्वारा परिभाषित वास्तविक मान फलन है। इस प्रकार के फलन को तत्समक फलन कहते हैं। यहाँ पर के प्रांत तथा परिसर हैं। इसका आलेख एक सरल रेखा होता है(चित्र-1)। यह रेखा मूल बिंदु से हो कर जाती है।
अचर फलन
जहाँ एक अचर है और प्रत्येक द्वारा परिभाषित एक वास्तविक मान फलन है। यहाँ पर का प्रांत है और उसका परिसर है। का आलेख - अक्ष के समांतर एक रेखा है, उदाहरण के लिए यदि प्रत्येक है, तो इसका आलेख (चित्र- 2) में दर्शाई रेखा है।
बहुपद फलन या बहुपदीय फलन
फलन , एक बहुपदीय फलन कहलाता है, यदि के प्रत्येक के लिए, , जहाँ ”" एक ऋणेतर पूर्णांक है तथा ।
, और , द्वारा परिभाषित फलन एक बहुपदीय फलन है जब कि द्वारा परिभाषित फलन , बहुपदीय फलन नहीं है।
परिमेय फलन
के प्रकार के फलन जहाँ तथा
एक प्रांत में, के परिभाषित बहुपदीय फलन हैं, जिसमें परिमेय फलन कहलाते हैं।
उदाहरण एक वास्तविक मान फलन की परिभाषा , द्वारा कीजिए। इस परिभाषा का प्रयोग करके निम्नलिखित तालिका को पूर्ण करेंगे। इस फलन का प्रांत तथा परिसर क्या हैं,इसका भी ज्ञात करेंगे।
हल पूर्ण की गई तालिका इस प्रकार है:
इसका प्रांत, शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं तथा इसका परिसर भी शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं। का आलेख चित्र-3 में प्रदर्शित है।
मापांक फलन
प्रत्येक द्वारा परिभाषित फलन , मापांक फलन कहलाता है। के प्रत्येक ऋणेत्तर मान के लिए , के समान होता है। परंतु के ऋण मानों के लिए, का मान के मान के ऋण के बराबर होता है,अर्थात्
मापांक फलन का आलेख चित्र-4 में दिया है । मापांक फलन को निरपेक्ष मान फलन भी कहते हैं।
चिह्न फलन
प्रत्येक , के लिए
, यदि
, यदि
, यदि
द्वारा परिभाषित फलन चिह्न फलन कहलाता है। चिह्न फलन का प्रांत है। परिसर समुच्चय है।
चित्र-5 में चिह्न फलन का आलेख दर्शाया गया है।
महत्तम पूर्णांक फलन
द्वारा परिभाषित फलन , से कम या के बराबर महत्तम पूर्णांक का मान ग्रहण (धारण) करता है ऐसा फलन महत्तम पूर्णांक फलन कहलाता है।
, की परिभाषा से हम देख सकते हैं कि
यदि
यदि
यदि
यदि इत्यदि
इस फलन का आलेख चित्र-6 में दर्शाया गया है।