सीमाएं: Difference between revisions
(added content) |
(added content) |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
गणित में सीमाओं को उन मानों के रूप में परिभाषित किया जाता है जो किसी फलन द्वारा दिए गए निवेश(इनपुट) मानों के लिए निर्गम(आउटपुट) तक पहुँचते हैं। सीमाएँ कलन और गणितीय विश्लेषण में महत्वपूर्ण भूमिका निभाती हैं और इनका उपयोग समाकलन, | गणित में सीमाओं को उन मानों के रूप में परिभाषित किया जाता है जो किसी फलन द्वारा दिए गए निवेश(इनपुट) मानों के लिए निर्गम(आउटपुट) तक पहुँचते हैं। सीमाएँ कलन और गणितीय विश्लेषण में महत्वपूर्ण भूमिका निभाती हैं और इनका उपयोग समाकलन, [[अवकलज]] और निरंतरता को परिभाषित करने के लिए किया जाता है। इसका उपयोग विश्लेषण प्रक्रिया में किया जाता है, और यह सदैव किसी विशेष बिंदु पर फलन के व्यवहार से संबंधित होता है। अनुक्रम की सीमा को टोपोलॉजिकल नेट की सीमा की अवधारणा में और अधिक सामान्यीकृत किया जाता है और सिद्धांत श्रेणी में सीमा और प्रत्यक्ष सीमा से संबंधित होता है। साधारणतः, समाकलन को दो प्रकारों में वर्गीकृत किया जाता है, अर्थात् निश्चित और अनिश्चित समाकलन। निश्चित समाकलन के लिए, ऊपरी सीमा और निम्न सीमा को ठीक से परिभाषित किया जाता है। जबकि अनिश्चित समाकलन बिना किसी सीमा के व्यक्त किए जाते हैं, और [[फलन]] को एकीकृत करते समय इसमें एक मनमाना स्थिरांक होगा। इस लेख में हम फलन की सीमाओं की परिभाषा और प्रतिनिधित्व पर विस्तार से चर्चा करें, गुणों और उदाहरणों के साथ। | ||
== परिभाषा == | == परिभाषा == | ||
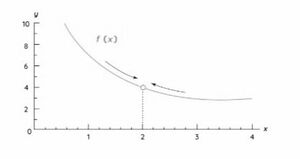
गणित में सीमाएँ अद्वितीय वास्तविक संख्याएँ होती हैं। आइए एक वास्तविक-मूल्यवान फलन | गणित में सीमाएँ अद्वितीय [[वास्तविक संख्याएँ]] होती हैं। आइए एक वास्तविक-मूल्यवान फलन “<math>f </math>” और वास्तविक संख्या “<math>c</math>” पर विचार करें, सीमा को सामान्य रूप से <math>\textstyle \lim_{x \to c} \displaystyle f(x)=L</math> के रूप में परिभाषित किया जाता है। इसे “<math>x</math> के <math>f </math> की सीमा, जैसे-जैसे <math>x</math>, <math>c</math> के करीब पहुँचता है <math>L</math> के बराबर होता है” के रूप में पढ़ा जाता है। “<math>lim</math>” सीमा को दर्शाता है, और तथ्य यह है कि फलन <math>f(x)</math> सीमा <math>L</math> के करीब पहुँचता है क्योंकि <math>x</math>, <math>c</math> के करीब पहुँचता है, इसे दाएँ तीर द्वारा वर्णित किया गया है।[[File:सीमाएं.jpg|thumb|चित्र- सीमाएं]] | ||
lim | |||
x | |||
c | |||
== सीमाएँ और फलन == | |||
फलन दो अलग-अलग सीमाओं तक पहुँच सकता है। एक जहाँ चर सीमा से बड़े मानों के माध्यम से अपनी सीमा तक पहुँचता है और दूसरा जहाँ चर सीमा से छोटे मानों के माध्यम से अपनी सीमा तक पहुँचता है। ऐसे स्थिति में, सीमा परिभाषित नहीं होती है लेकिन दाएँ और बाएँ हाथ की सीमाएँ उपस्थित होती हैं। | |||
x | जब <math> \textstyle \lim_{x \to a} \displaystyle f(x)=A^+</math> <math>a</math> के दाएँ <math>x</math> के निकट <math>f </math> के मान दिए गए हैं। इस मान को <math>a</math> पर <math>f(x)</math> की दाएँ हाथ की सीमा कहा जाता है। | ||
) | जब <math> \textstyle \lim_{x \to a} \displaystyle f(x)=A^-</math> <math>a</math> के बाएँ <math>x</math> के निकट <math>f </math> के मान दिए गए हैं। इस मान को <math>a</math> पर <math>f(x)</math> की बाएँ हाथ की सीमा कहा जाता है। | ||
फलन की सीमा तभी उपस्थित होती है जब बाएँ हाथ की सीमा दाएँ हाथ की सीमा के बराबर हो। | |||
L | <math> \textstyle \lim_{x \to a^{-1}} \displaystyle f(x)=\textstyle \lim_{x \to a^{+}} \displaystyle f(x)= L</math> | ||
नोट: फलन की सीमा किसी भी दो लगातार [[पूर्णांक|पूर्णांकों]] के बीच उपस्थित होती है। | |||
नोट: फलन | |||
== सीमाओं के गुणधर्म == | == सीमाओं के गुणधर्म == | ||
फलन की सीमाओं के कुछ गुण इस प्रकार हैं: यदि सीमाएँ | फलन की सीमाओं के कुछ गुण इस प्रकार हैं: यदि सीमाएँ | ||
<math> \textstyle \lim_{x \to a} \displaystyle f(x)</math>और <math> \textstyle \lim_{x \to a} \displaystyle g(x)</math> उपस्थित हैं, और <math> n</math> एक पूर्णांक है, तो, | |||
x | |||
a | |||
f(x) और | |||
x | |||
a | |||
g(x) | |||
'''जोड़ने का नियम''': | '''जोड़ने का नियम''': | ||
<math> \textstyle \lim_{x \to a} \displaystyle [f(x)+g(x)]=\textstyle \lim_{x \to a} \displaystyle f(x) + \textstyle \lim_{x \to a} \displaystyle g(x) </math> | |||
x | |||
a | |||
[ | |||
f | |||
( | |||
x | |||
) | |||
+ | |||
g | |||
( | |||
x | |||
) | |||
] | |||
= | |||
x | |||
a | |||
f | |||
( | |||
x | |||
) | |||
+ | |||
x | |||
a | |||
g | |||
( | |||
x | |||
) | |||
'''घटाने का नियम''': | '''घटाने का नियम''': | ||
<math> \textstyle \lim_{x \to a} \displaystyle [f(x)-g(x)]=\textstyle \lim_{x \to a} \displaystyle f(x)- \textstyle \lim_{x \to a} \displaystyle g(x) </math> | |||
x | |||
a | |||
[ | |||
f | |||
( | |||
x | |||
) | |||
g | |||
( | |||
x | |||
) | |||
] | |||
= | |||
x | |||
a | |||
f | |||
( | |||
x | |||
) | |||
x | |||
a | |||
g | |||
( | |||
x | |||
) | |||
'''गुणन का नियम''': | '''गुणन का नियम''': | ||
<math> \textstyle \lim_{x \to a} \displaystyle [f(x) \cdot g(x)]=\textstyle \lim_{x \to a} \displaystyle f(x) \cdot \textstyle \lim_{x \to a} \displaystyle g(x) </math> | |||
x | |||
a | |||
[ | |||
f | |||
( | |||
x | |||
) | |||
g | |||
( | |||
x | |||
) | |||
] | |||
= | |||
x | |||
a | |||
f | |||
( | |||
x | |||
) | |||
x | |||
a | |||
g | |||
( | |||
x | |||
) | |||
'''विभाजन का नियम''': | '''विभाजन का नियम''': | ||
<math> \textstyle \lim_{x \to a} \displaystyle \Bigl(\frac{f(x)}{g(x)}\Bigr)= \frac{\textstyle \lim_{x \to a} \displaystyle f(x)}{\textstyle \lim_{x \to a} \displaystyle g(x)} </math> ,जहाँ <math> \textstyle \lim_{x \to a} \displaystyle g(x)\neq 0</math> | |||
x | |||
'''घात का नियम''': | |||
<math> \textstyle \lim_{x \to a} \displaystyle c=c</math> | |||
x | |||
a | |||
c | |||
= | |||
c | |||
== विशेष नियम: == | == विशेष नियम: == | ||
1. | 1. <math> \textstyle \lim_{x \to a} \displaystyle \frac{x^n-a^n}{x-a}=na^{n-1}</math>, <math>n</math> के सभी वास्तविक मानों के लिए. | ||
2. | 2. <math> \textstyle \lim_{\theta \to 0} \displaystyle\frac{ sin\theta}{\theta}=1</math> | ||
3. | 3. <math> \textstyle \lim_{\theta \to 0} \displaystyle\frac{ tan\theta}{\theta}=1</math> | ||
4. | 4. <math> \textstyle \lim_{\theta \to 0} \displaystyle\frac{ 1-cos\theta}{\theta}=0</math> | ||
5. | 5. <math> \textstyle \lim_{\theta \to 0} \displaystyle cos\theta=1</math> | ||
6. | 6. <math> \textstyle \lim_{x \to 0} \displaystyle e^x=1</math> | ||
7. | 7. <math> \textstyle \lim_{x \to 0} \displaystyle\frac{ e^x-1}{x}=1</math> | ||
8. | 8. <math> \textstyle \lim_{x \to \infty} \displaystyle\Bigl({1+\frac{1}{x}\Bigr)^x}=e</math> | ||
== दो चरों वाले फलन | == दो चरों वाले फलन की सीमा == | ||
यदि हमारे पास एक फलन f(x, y) है जो दो चर x और y पर निर्भर करता है, तो इस दिए गए फलन की सीमा, मान लीजिए, C है (x,y) | यदि हमारे पास एक फलन <math>f(x, y)</math> है जो दो चर <math>x</math> और <math>y</math> पर निर्भर करता है, तो इस दिए गए फलन की सीमा, मान लीजिए, <math>C</math> है<math>(x,y)\rightarrow(a,b)</math> मान लीजिए कि <math>\in > 0, \vartriangle > 0</math> उपस्थित है जैसे कि <math>|f(x, y)-C| < \in</math> जब भी <math>0 < \sqrt{(x-a)^2+(y-b)^2} < \vartriangle</math>। इसे इस प्रकार <math>\textstyle \lim_{(x,y) \to (a,b)} \displaystyle f(x,y) = C</math> परिभाषित किया गया है । | ||
== फलन की सीमाएँ और निरंतरता == | |||
== फलन | |||
फलन की सीमाएँ और फलन की निरंतरता एक दूसरे से निकटता से संबंधित हैं। फलन निरंतर या असंतत हो सकते हैं। किसी फलन के निरंतर होने के लिए, यदि फलन के इनपुट में छोटे परिवर्तन हैं तो आउटपुट में भी छोटे परिवर्तन होने चाहिए। | फलन की सीमाएँ और फलन की निरंतरता एक दूसरे से निकटता से संबंधित हैं। फलन निरंतर या असंतत हो सकते हैं। किसी फलन के निरंतर होने के लिए, यदि फलन के इनपुट में छोटे परिवर्तन हैं तो आउटपुट में भी छोटे परिवर्तन होने चाहिए। | ||
प्राथमिक कलन में, शर्त f( | प्राथमिक कलन में, शर्त <math>f(x)\rightarrow \lambda</math> जैसे कि <math>x\rightarrow a</math> का अर्थ है कि संख्या <math>f(x)</math> को संख्या <math>\lambda</math> के जितना करीब चाहें उतना रखा जा सकता है, बशर्ते हम संख्या को संख्या <math>a</math> के बराबर न लें लेकिन <math>a</math> के काफी करीब रखें। जो दर्शाता है कि<math>f(a)</math> <math>\lambda</math> से बहुत दूर हो सकता है और <math>f(a)</math> को परिभाषित करने की भी कोई आवश्यकता नहीं है। फलन की व्युत्पत्ति के लिए हम जो बहुत महत्वपूर्ण परिणाम उपयोग करते हैं वह है: किसी संख्या <math>a</math> पर दिए गए फलन <math>f</math> का <math>f'(a)</math> इस प्रकार माना जा सकता है, | ||
f'(a) = | <math>f'(a) =\textstyle \lim_{x \to a} \displaystyle \frac{f(x)-f(a)}{x-a}</math> | ||
== सम्मिश्र फलन की सीमाएँ == | |||
किसी सम्मिश्र चर के कार्यों को विभेदित करने के लिए नीचे दिए गए सूत्र का पालन करें: | |||
फलन <math>f(z)</math> को <math>z=z_0</math> पर अवकलनीय कहा जाता है यदि | |||
<math>\textstyle \lim_{\displaystyle \vartriangle z \to 0} \frac{f(z_0+\vartriangle z)-f(z_0)}{\vartriangle z}</math> विद्यमान है। | |||
यहाँ <math>\vartriangle z=\vartriangle x+i\vartriangle y</math> | |||
== घातांकीय फलनों की सीमाएँ == | |||
किसी भी वास्तविक संख्या <math>x</math> के लिए, आधार <math>a</math> के साथ घातांकीय फलन<math>f (x) = a^x</math> है जहाँ <math>a >0</math> है और <math>a</math> शून्य के बराबर नहीं है। घातांकीय फलनों की सीमाओं से निपटने के दौरान उपयोग किए जाने वाले सीमाओं के कुछ महत्वपूर्ण नियम नीचे दिए गए हैं। | |||
== | |||
किसी | |||
फलन | |||
f | |||
( | |||
) | |||
= | |||
0 | |||
<math>f(b) >1</math> के लिए | |||
* <math>\textstyle \lim_{x \to \infty} \displaystyle b^x=\infty</math> | |||
* <math>\textstyle \lim_{x \to -\infty} \displaystyle b^x=0</math> | |||
<math>0<b<1</math> के लिए | |||
* <math>\textstyle \lim_{x \to \infty} \displaystyle b^x=0</math> | |||
* <math>\textstyle \lim_{x \to -\infty} \displaystyle b^x=\infty</math> | |||
== उदाहरण == | |||
फलन की सीमा ज्ञात करें। | |||
== | |||
<math>\textstyle \lim_{x \to 0} \displaystyle \frac{(tan x)}{(sin x)}</math> | |||
'''समाधान''': <math>\textstyle \lim_{x \to 0} \displaystyle \frac{(tan x)}{(sin x)}</math> | |||
हम जानते हैं, <math>tan x = \frac{ sin x}{cos x}</math> | |||
<math>=\textstyle \lim_{x \to 0} \displaystyle \Bigl(\frac{1}{cos x}\Bigr)= 1</math> | |||
'''उत्तर''': सीमा <math>\textstyle \lim_{x \to 0} \displaystyle \frac{(tan x)}{(sin x)}=1</math> | |||
[[Category:सीमा और अवकलज]][[Category:कक्षा-11]][[Category:गणित]] | [[Category:सीमा और अवकलज]][[Category:कक्षा-11]][[Category:गणित]] | ||
Latest revision as of 23:12, 23 November 2024
गणित में सीमाओं को उन मानों के रूप में परिभाषित किया जाता है जो किसी फलन द्वारा दिए गए निवेश(इनपुट) मानों के लिए निर्गम(आउटपुट) तक पहुँचते हैं। सीमाएँ कलन और गणितीय विश्लेषण में महत्वपूर्ण भूमिका निभाती हैं और इनका उपयोग समाकलन, अवकलज और निरंतरता को परिभाषित करने के लिए किया जाता है। इसका उपयोग विश्लेषण प्रक्रिया में किया जाता है, और यह सदैव किसी विशेष बिंदु पर फलन के व्यवहार से संबंधित होता है। अनुक्रम की सीमा को टोपोलॉजिकल नेट की सीमा की अवधारणा में और अधिक सामान्यीकृत किया जाता है और सिद्धांत श्रेणी में सीमा और प्रत्यक्ष सीमा से संबंधित होता है। साधारणतः, समाकलन को दो प्रकारों में वर्गीकृत किया जाता है, अर्थात् निश्चित और अनिश्चित समाकलन। निश्चित समाकलन के लिए, ऊपरी सीमा और निम्न सीमा को ठीक से परिभाषित किया जाता है। जबकि अनिश्चित समाकलन बिना किसी सीमा के व्यक्त किए जाते हैं, और फलन को एकीकृत करते समय इसमें एक मनमाना स्थिरांक होगा। इस लेख में हम फलन की सीमाओं की परिभाषा और प्रतिनिधित्व पर विस्तार से चर्चा करें, गुणों और उदाहरणों के साथ।
परिभाषा
गणित में सीमाएँ अद्वितीय वास्तविक संख्याएँ होती हैं। आइए एक वास्तविक-मूल्यवान फलन “” और वास्तविक संख्या “” पर विचार करें, सीमा को सामान्य रूप से के रूप में परिभाषित किया जाता है। इसे “ के की सीमा, जैसे-जैसे , के करीब पहुँचता है के बराबर होता है” के रूप में पढ़ा जाता है। “” सीमा को दर्शाता है, और तथ्य यह है कि फलन सीमा के करीब पहुँचता है क्योंकि , के करीब पहुँचता है, इसे दाएँ तीर द्वारा वर्णित किया गया है।
सीमाएँ और फलन
फलन दो अलग-अलग सीमाओं तक पहुँच सकता है। एक जहाँ चर सीमा से बड़े मानों के माध्यम से अपनी सीमा तक पहुँचता है और दूसरा जहाँ चर सीमा से छोटे मानों के माध्यम से अपनी सीमा तक पहुँचता है। ऐसे स्थिति में, सीमा परिभाषित नहीं होती है लेकिन दाएँ और बाएँ हाथ की सीमाएँ उपस्थित होती हैं।
जब के दाएँ के निकट के मान दिए गए हैं। इस मान को पर की दाएँ हाथ की सीमा कहा जाता है।
जब के बाएँ के निकट के मान दिए गए हैं। इस मान को पर की बाएँ हाथ की सीमा कहा जाता है।
फलन की सीमा तभी उपस्थित होती है जब बाएँ हाथ की सीमा दाएँ हाथ की सीमा के बराबर हो।
नोट: फलन की सीमा किसी भी दो लगातार पूर्णांकों के बीच उपस्थित होती है।
सीमाओं के गुणधर्म
फलन की सीमाओं के कुछ गुण इस प्रकार हैं: यदि सीमाएँ
और उपस्थित हैं, और एक पूर्णांक है, तो,
जोड़ने का नियम:
घटाने का नियम:
गुणन का नियम:
विभाजन का नियम:
,जहाँ
घात का नियम:
विशेष नियम:
1. , के सभी वास्तविक मानों के लिए.
2.
3.
4.
5.
6.
7.
8.
दो चरों वाले फलन की सीमा
यदि हमारे पास एक फलन है जो दो चर और पर निर्भर करता है, तो इस दिए गए फलन की सीमा, मान लीजिए, है मान लीजिए कि उपस्थित है जैसे कि जब भी । इसे इस प्रकार परिभाषित किया गया है ।
फलन की सीमाएँ और निरंतरता
फलन की सीमाएँ और फलन की निरंतरता एक दूसरे से निकटता से संबंधित हैं। फलन निरंतर या असंतत हो सकते हैं। किसी फलन के निरंतर होने के लिए, यदि फलन के इनपुट में छोटे परिवर्तन हैं तो आउटपुट में भी छोटे परिवर्तन होने चाहिए।
प्राथमिक कलन में, शर्त जैसे कि का अर्थ है कि संख्या को संख्या के जितना करीब चाहें उतना रखा जा सकता है, बशर्ते हम संख्या को संख्या के बराबर न लें लेकिन के काफी करीब रखें। जो दर्शाता है कि से बहुत दूर हो सकता है और को परिभाषित करने की भी कोई आवश्यकता नहीं है। फलन की व्युत्पत्ति के लिए हम जो बहुत महत्वपूर्ण परिणाम उपयोग करते हैं वह है: किसी संख्या पर दिए गए फलन का इस प्रकार माना जा सकता है,
सम्मिश्र फलन की सीमाएँ
किसी सम्मिश्र चर के कार्यों को विभेदित करने के लिए नीचे दिए गए सूत्र का पालन करें:
फलन को पर अवकलनीय कहा जाता है यदि
विद्यमान है।
यहाँ
घातांकीय फलनों की सीमाएँ
किसी भी वास्तविक संख्या के लिए, आधार के साथ घातांकीय फलन है जहाँ है और शून्य के बराबर नहीं है। घातांकीय फलनों की सीमाओं से निपटने के दौरान उपयोग किए जाने वाले सीमाओं के कुछ महत्वपूर्ण नियम नीचे दिए गए हैं।
के लिए
के लिए
उदाहरण
फलन की सीमा ज्ञात करें।
समाधान:
हम जानते हैं,
उत्तर: सीमा