|
|
| (2 intermediate revisions by the same user not shown) |
| Line 75: |
Line 75: |
|
| |
|
| == उदाहरण == | | == उदाहरण == |
| '''समस्या''' 1- <math>sin^{-1 }(sin (4)</math> का मान क्या है? | | '''प्रश्न 1''' <math>6 sin^{-1}1</math> का मान |
|
| |
|
| '''समाधान''' 1- जैसा कि हम जानते हैं, <math>sin^{-1} (sin x) = x</math> | | '''उत्तर''': मान लीजिए <math>A=sin^{-1}1,</math> तो <math>sinA=1</math> |
|
| |
|
| इसलिए,<math>sin^{-1 }(sin (4)</math> का मान <math>x</math><math>tan^{-1}211 + tan^{-1}724= tan^{-1}12</math><math>= 4</math>
| | चूँकि <math>sin \frac{\pi}{2}=1,</math> |
|
| |
|
| समस्या 2- सिद्ध करें कि <math>tan^{-1}211 + tan^{-1}724= tan^{-1}12</math>
| | <math>6sin^{-1}1=6\times\frac{\pi}{2}</math> |
|
| |
|
| समाधान 2- <math>tan^{-1}x + tan^{-1}y= tan^{-1}x+y^1-xy</math>
| | <math>6sin^{-1}1=3\pi</math> |
|
| |
|
| <math>tan^{-1}211 + tan^{-1}724= tan^{-1}211+7241-211\cdot724</math>
| |
|
| |
|
| <math>= tan^{-1}48+7724\times1111\times24-1424\times11 = tan^{-1}125250</math> | | '''प्रश्न 2''' <math>tan^{-1}(1.1106)</math> का मान ज्ञात करें। |
|
| |
|
| <math>= tan^{-1}12</math> | | '''उत्तर''': मान लें <math>A=tan^{-1}(1.1106)</math> |
|
| |
|
| इसलिए, हम सत्यापित कर सकते हैं कि
| | तो, <math>tanA = 1.1106</math> |
|
| |
|
| '''समस्या''' 3 <math>sin^{-1}-12</math> का मुख्य मान क्या है?
| | <math>A=48^\circ</math> |
|
| |
|
| '''समाधान''' 3
| | <math>tan48 = 1.1106</math> |
|
| |
|
| हम जानते हैं कि <math>-1</math> से <math>1</math> की सीमा में आने वाले के सभी मानों के लिए, <math>sin^{-1}(-x) = -sin^{-1} x</math> ।
| | [डिग्री मोड में कैलकुलेटर का उपयोग करें] |
|
| |
|
| इसलिए, <math>y = sin^{-1}-12</math><math>y = sin^{-1}-12</math>
| | <math>tan^{-1}(1.1106)=48^\circ</math> |
|
| |
|
| चूँकि, <math>sin 6 = 12</math>
| | == महत्वपूर्ण टिप्पणियाँ == |
| | नीचे दिए गए कुछ सुझाव प्रतिलोम त्रिकोणमितीय फलनों के विभिन्न सूत्रों को हल करने और लागू करने में सहायक होंगे। |
|
| |
|
| इसलिए, <math>sin^{-1}12 = 6</math>
| | * <math>sin^{-1}(sin x) = x, |
| | </math> जब <math>-1 \leq x \leq 1</math> (अधिक जानकारी के लिए, यहाँ क्लिक करें) |
| | * <math>sin(sin^{-1}x) = x, |
| | </math> जब <math> \frac{-\pi}{2} \leq x \leq \frac{\pi}{2}</math> |
| | * <math>sin^{-1}x |
| | </math> , <math> (sin x)^{-1} |
| | </math>से अलग है। साथ ही, <math>(sin x)^{-1}= \frac{1}{sinx}</math> |
| | * <math>sin^{-1}x = \theta</math> और <math>\theta</math> कोण को संदर्भित करता है, जो इस प्रतिलोम त्रिकोणमितीय फलनों का मुख्य मान है। |
|
| |
|
| इसलिए, <math>y = sin^{-1}-sin 6 = 6</math>
| |
|
| |
| इसलिए, <math>sin^{-1}-12</math> का मुख्य मान <math>= 6</math>
| |
|
| |
| == निष्कर्ष ==
| |
| प्रतिलोम त्रिकोणमिति की अवधारणा त्रिकोणमितीय फलनों के प्रतिलोम फलनों से संबंधित है। इसलिए, प्रतिलोम त्रिकोणमितीय फलन प्रतिलोम कोटैंजेंट, प्रतिलोम कोसेकेंट, प्रतिलोम साइन, प्रतिलोम स्पर्शज्या, प्रतिलोम सेकेंट और प्रतिलोम कोसाइन हैं।
| |
|
| |
| जब समकोण त्रिभुज की केवल दो भुजाएँ ज्ञात हों, तो प्रतिलोम त्रिकोणमितीय फलन कोण माप निर्धारित करते हैं। प्रतिलोम त्रिकोणमितीय फलनों की अवधारणा का उपयोग प्रायः भौतिकी, ज्यामिति, इंजीनियरिंग आदि में किया जाता है। प्रतिलोम त्रिकोणमितीय फलनों को त्रिकोणमितीय-विरोधी फलन या आर्कस फलन के रूप में भी जाना जाता है।
| |
| [[Category:गणित]][[Category:गणित]][[Category:कक्षा-12]][[Category:कक्षा-12]] | | [[Category:गणित]][[Category:गणित]][[Category:कक्षा-12]][[Category:कक्षा-12]] |
| [[Category:अवकल समीकरण]] | | [[Category:अवकल समीकरण]] |
प्रतिलोम त्रिकोणमितीय फलन, आर्कस फलन या प्रति त्रिकोणमितीय फलन होते हैं। ये त्रिकोणमितीय फलनों के प्रतिलोम फलन हैं, जिनके प्रांत(डोमेन) उपयुक्त रूप से सीमित होते हैं। यहाँ, हम साइन, कोसाइन, टैन्जन्ट , कोटैन्जन्ट , सेकेंट और कोसेकेंट फलनों के लिए प्रतिलोम त्रिकोणमितीय सूत्रों का अध्ययन करेंगे।
परिचय
गणित की वह शाखा जो कोणों और भुजाओं से संबंधित है, त्रिकोणमिति कहलाती है।
प्रतिलोम त्रिकोणमितीय फलनों की अवधारणा त्रिकोणमितीय फलनों के प्रतिलोम फलनों से संबंधित है। इसलिए, प्रतिलोम त्रिकोणमितीय फलन, प्रतिलोम कोटैंजेंट, प्रतिलोम कोसेकेंट, प्रतिलोम साइन, प्रतिलोम स्पर्शज्या, प्रतिलोम सेकेंट और प्रतिलोम कोसाइन हैं।
जब समकोण त्रिभुज की केवल दो भुजाएँ ज्ञात हों, तो प्रतिलोम त्रिकोणमितीय फलन कोण माप निर्धारित करते हैं।
प्रतिलोम त्रिकोणमितीय फलनों की अवधारणा का उपयोग साधारणतः भौतिकी, ज्यामिति, इंजीनियरिंग आदि में किया जाता है।
प्रतिलोम त्रिकोणमितीय फलनों को त्रिकोणमितीय विरोधी फलन या आर्कस फलन भी कहा जाता है।
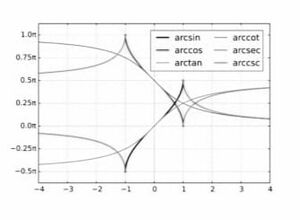
चित्र प्रतिलोम त्रिकोणमितीय फलन
प्रतिलोम त्रिकोणमितीय सूत्र
प्रतिलोम त्रिकोणमितीय फलन त्रिकोणमितीय फलनों के प्रतिलोम फलन होते हैं जिन्हें  के रूप में लिखा जाता है।
के रूप में लिखा जाता है।
प्रतिलोम त्रिकोणमितीय फलन बहु-मूल्यवान होते हैं। उदाहरण के लिए,  के कई मान ऐसे हैं कि
के कई मान ऐसे हैं कि  , इसलिए
, इसलिए  तब तक विशिष्ट रूप से परिभाषित नहीं होता जब तक कि कोई मुख्य मान परिभाषित न हो। ऐसे मुख्य मानों को कभी-कभी बड़े अक्षर से दर्शाया जाता है, इसलिए, उदाहरण के लिए, प्रतिलोम साइन के मुख्य मान को
तब तक विशिष्ट रूप से परिभाषित नहीं होता जब तक कि कोई मुख्य मान परिभाषित न हो। ऐसे मुख्य मानों को कभी-कभी बड़े अक्षर से दर्शाया जाता है, इसलिए, उदाहरण के लिए, प्रतिलोम साइन के मुख्य मान को  या
या  ) के रूप में विभिन्न रूप से दर्शाया जा सकता है।
) के रूप में विभिन्न रूप से दर्शाया जा सकता है।
मान लीजिए, यदि  तो
तो  , इसी तरह अन्य त्रिकोणमितीय कार्यों के लिए भी। यह प्रतिलोम त्रिकोणमितीय सूत्रों में से एक है। अब,
, इसी तरह अन्य त्रिकोणमितीय कार्यों के लिए भी। यह प्रतिलोम त्रिकोणमितीय सूत्रों में से एक है। अब,
![{\displaystyle ,y\in [{\frac {\pi }{2}},{\frac {\pi }{2}}]}](/index.php?title=Special:MathShowImage&hash=6494c847cf61b5eca088480505e9276d&mode=mathml) और
और ![{\displaystyle x\in [-1,1]}](/index.php?title=Special:MathShowImage&hash=950f94b68fe52b9679fb231b15234515&mode=mathml) ।
।
इस प्रकार, दिए गए ![{\displaystyle x\in [-1,1]}](/index.php?title=Special:MathShowImage&hash=950f94b68fe52b9679fb231b15234515&mode=mathml) के लिए
के लिए  के अनंत मान हैं।
के अनंत मान हैं।
इन मानों में से केवल एक मान है जो अंतराल ![{\displaystyle [{\frac {\pi }{2}},{\frac {\pi }{2}}]}](/index.php?title=Special:MathShowImage&hash=a282ad295907e7bd48440da94004430d&mode=mathml) में स्थित है। इस मान को मुख्य मान कहा जाता है।
में स्थित है। इस मान को मुख्य मान कहा जाता है।
प्रतिलोम त्रिकोणमितीय सर्वसमिकाएँ
जबकि प्रतिलोम त्रिकोणमितीय फलनों के केवल छह गुण हैं, फिर भी कुछ प्रतिलोम त्रिकोणमितीय पहचान और प्रतिलोम त्रिकोणमिति सूत्र हैं जिन्हें अनदेखा कर दिया गया है। इसलिए, निम्नलिखित सूची में कुछ और प्रतिलोम त्रिकोणमितीय सर्वसमिकाएँ हैं-







![{\displaystyle cos^{-1}x+cos^{-1}y=cos^{-1}[xy-{\sqrt {(1-x^{2})(1-y^{2})}}]}](/index.php?title=Special:MathShowImage&hash=623cbe26a27fbc246c92b7594cc00345&mode=mathml)
![{\displaystyle cos^{-1}x-cos^{-1}y=cos^{-1}[xy+{\sqrt {(1-x^{2})(1-y^{2})}}]}](/index.php?title=Special:MathShowImage&hash=b4671a98cc4c5065132d04ea692bad68&mode=mathml)



व्युत्क्रम त्रिकोणमितीय फलन परिसर और प्रांत तालिका
| फलन
|
परिसर
|
प्रांत
|
| y = sin-1 x
|
-2 , 2
|
-1, 1
|
| y = cos-1 x
|
0, π
|
-1, 1
|
| y = cosec-1 x
|
-2 , 2
|
R – (-1, 1)
|
| y = sec-1 x
|
0, π- 2
|
R – (-1, 1)
|
| y = tan-1 x
|
-2 , 2
|
R
|
| y = cot-1 x
|
0, π
|
R
|
उदाहरण
प्रश्न 1  का मान
का मान
उत्तर: मान लीजिए  तो
तो 
चूँकि 


प्रश्न 2  का मान ज्ञात करें।
का मान ज्ञात करें।
उत्तर: मान लें 
तो, 


[डिग्री मोड में कैलकुलेटर का उपयोग करें]

महत्वपूर्ण टिप्पणियाँ
नीचे दिए गए कुछ सुझाव प्रतिलोम त्रिकोणमितीय फलनों के विभिन्न सूत्रों को हल करने और लागू करने में सहायक होंगे।
 जब
जब  (अधिक जानकारी के लिए, यहाँ क्लिक करें)
(अधिक जानकारी के लिए, यहाँ क्लिक करें) जब
जब 
 ,
,  से अलग है। साथ ही,
से अलग है। साथ ही, 
 और
और  कोण को संदर्भित करता है, जो इस प्रतिलोम त्रिकोणमितीय फलनों का मुख्य मान है।
कोण को संदर्भित करता है, जो इस प्रतिलोम त्रिकोणमितीय फलनों का मुख्य मान है।
