चरघातांकी तथा लघूगणकीय फलन: Difference between revisions
(formulas) |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
चरघातांकी और लघुगणकीय फलन | चरघातांकी और लघुगणकीय फलन संभवतः सबसे महत्वपूर्ण फलन हैं जिनका सामना आपको किसी भौतिक समस्या से निपटने के दौरान करना होगा। वे एक दूसरे के व्युत्क्रम या प्रतिलोम हैं और संख्याओं की एक बड़ी श्रृंखला को बहुत आसानी से दर्शाने के लिए उपयोग किया जा सकता है। | ||
वे अपने पूरे | वे अपने पूरे प्रांत में सांतत्य और अवकलनीय हैं, और उनके [[अवकलज|अवकलजों]] के संकेतन में सरलता, आपको गणित के साथ-साथ अन्य विषयों में उनके विशाल महत्व के बारे में एक विचार देगी। आइए अब हम इन फलनों को व्यक्तिगत रूप से समझते हैं, उनके बीच संबंध पर आगे बढ़ने से पहले। | ||
== चरघातांकी फलन == | == चरघातांकी फलन == | ||
'घातांक' शब्द का तात्पर्य किसी संख्या की 'घात' से है। उदाहरण के लिए - संख्या | 'घातांक' शब्द का तात्पर्य किसी संख्या की '[[घात समुच्चय|घात]]' से है। उदाहरण के लिए - संख्या <math> 2^3</math> में 2 का घातांक 3 के बराबर है। स्पष्ट रूप से, चरघातांकी फलन वे होते हैं जहाँ चर घात के रूप में होता है। चरघातांकी फलन को इस प्रकार परिभाषित किया जाता है- | ||
<math>f(x)=a^x</math> | <math>f(x)=a^x</math> | ||
जहाँ <math>a</math> एक धनात्मक वास्तविक संख्या है, जो <math>1</math> के बराबर नहीं है। | जहाँ <math>a</math> एक धनात्मक [[वास्तविक संख्याएँ|वास्तविक संख्या]] है, जो <math>1</math> के बराबर नहीं है। | ||
यदि <math>a = 1,</math> तो <math>f(x) = 1^x,</math> जो <math>1</math>, <math>\forall x</math> के बराबर है। इसलिए फलन का | यदि <math>a = 1,</math> तो <math>f(x) = 1^x,</math> जो <math>1</math>, <math>\forall x</math> के बराबर है। इसलिए फलन का आलेख स्थिरांक <math>y (= 1)</math> की एक सरल रेखा होगी। ‘<math>a</math>’ के मान के आधार पर, हमारे पास दो संभावित स्थितियाँ हो सकते हैं: | ||
स्थिति 1: <math>a > 1</math> | |||
[[File:चरघातांकी फलन-1.jpg|thumb|चरघातांकी फलन-1]] | |||
यहाँ, चरघातांकी फलन <math>x</math> के बढ़ने के साथ बहुत तेज़ी से बढ़ता है और <math>x</math> के <math>+\infty</math> की ओर बढ़ने पर <math>+\infty</math> की ओर बढ़ता है। जब <math>x = 0, a^x = 1;</math>और जब <math>x</math>, <math>-\infty</math> की ओर बढ़ता है, तो फलन <math>0</math> की ओर बढ़ता है। फलन का सामान्य आलेख इस तरह दिखता है: (जहाँ <math>a = 2</math>) | |||
स्थिति 2: <math>a < 1</math> | |||
[[File:चरघातांकी फलन-2.jpg|thumb|चरघातांकी फलन-2]] | |||
फलन <math>x</math> के बढ़ने के साथ बहुत तेज़ी से घटता है और <math>x</math> के <math>+\infty</math> की ओर बढ़ने पर <math>0</math> की ओर बढ़ता है। जब <math>x = 0, a^x = 1;</math> सदैव की तरह; और जब <math>x</math>, <math>-\infty</math> की ओर बढ़ता है, तो फलन <math>+\infty</math> की ओर बढ़ता है। ऐसे फलन का सामान्य आलेख इस तरह दिखता है - (जहाँ <math>a = 2</math> फिर से) | |||
== चरघातांकी फलनों के गुण == | |||
* चरघातांकी [[फलन]] का प्रांत <math>(-\infty,+\infty)</math> है, अर्थात इसे <math>\forall x</math> से परिभाषित किया जाता है। | |||
* चरघातांकी फलन की सीमा <math>(0,+\infty)</math> है। यह गुण <math>a^x</math> फलन के आलेख से स्पष्ट होना चाहिए। अन्यथा, यह भी तर्कसंगत है कि किसी भी वास्तविक संख्या की घात ऋणात्मक संख्या नहीं हो सकती। मात्र काल्पनिक संख्याओं में ही ऐसा व्यवहार हो सकता है। | |||
* बिंदु <math>(0,1)</math>और<math>(1, a)</math> सदैव <math>a^x</math> फलन के आलेख पर स्थित होते हैं। | |||
* ‘<math>a</math>’ अनिवार्य रूप से एक धनात्मक संख्या होनी चाहिए। यदि <math>a</math> एक ऋणात्मक संख्या है, तो <math>x</math> के किसी भी भिन्नात्मक मान के लिए, हमें परिणाम के रूप में एक काल्पनिक संख्या मिलेगी जिसे उसी आलेख पर आलेखित नहीं किया जा सकता है। उदाहरण के लिए- <math>(-2)^{\frac{1}{2}} = \sqrt{2}i</math> | |||
* गुणनफल नियम – | |||
<math> a^x\cdot a^y=a^{x+y}</math> | |||
* भागफल नियम – | |||
<math> \frac{a^x}{a^y} =a^{x-y}</math> | |||
* चरघातांकी फलन अपने पूरे प्रांत में संतत और अवकलनीय है। अवकलज इस प्रकार दिया गया है | |||
<math>{d(a^x) \over dx}=a^x \ln (a)</math> | |||
जहाँ <math>\ln (a)</math> या <math>log_e(a), a </math> का प्राकृतिक लघुगणक है। हम इसे कुछ समय में औपचारिक रूप से परिभाषित करेंगे। मानक चरघातांकी फलन <math> e^x</math> गणित में एक अद्वितीय फलन है जिसमें इसके अवकलज के बराबर होने का गुण होता है। इस प्रकार, हमारे पास है | |||
<math>{d(e^x) \over dx}=e^x</math> | |||
वास्तव में, इन अवकलजों के पीछे की गणना संख्या ‘<math>e </math>’ को परिभाषित करने के तरीकों में से एक है जो <math>2.71828</math> के बराबर है… अभी के लिए चरघातांकी फलनों के बारे में इतना ही। | |||
== लघुगणकीय फलन == | |||
चूँकि हमने पहले ही उजागर कर दिया था कि लघुगणक फलन और चरघातांकी फलन एक दूसरे के प्रतिलोम हैं, इसलिए यह स्पष्ट होना चाहिए कि लघुगणक फलन ‘किसी संख्या की घात लेने’ के विपरीत फलन करता है। आइए इसे गणितीय रूप से देखें – | |||
सामान्य संकेतन | |||
* घातांकीय रूप – | |||
<math>b^y = x</math> | |||
* लघुगणकीय रूप – | |||
<math> y=\log_{b}x</math> जहाँ ‘<math> b</math>’ लघुगणक <math> \log</math> का आधार है। | |||
इन दो रूपों के साथ, आप आसानी से देख सकते हैं कि फलन <math> f(x)= \log_{b}x</math> का मान वह घात है जिस तक ‘<math> b</math>’ को बढ़ाकर ‘<math> x</math>’ प्राप्त करना होगा। इसलिए, ‘<math> x</math>’ ऋणात्मक नहीं हो सकता क्योंकि इसके लिए ‘<math> b</math>’ को काल्पनिक होना आवश्यक है, आधार ‘<math> b</math>’ पर स्थितियाँ – | |||
* <math> b > 0</math>: यह लघूगणकीय फलन के चरघातांकी निरूपण से सीधे अनुसरण करता है। | |||
* <math> b \neq 1</math>: चूँकि 1 को किसी भी घात तक बढ़ाने पर केवल 1 ही प्राप्त होगा। | |||
‘<math> b</math>’ के मान के आधार पर, हमारे पास दो संभावित मामले होंगे – | |||
स्थिति 1: <math> b > 1</math> | |||
[[File:लघुगणकीय फलन-1.jpg|thumb|लघुगणकीय फलन-1]] | |||
यहाँ, लघूगणकीय फलन <math> x</math> के घटने के साथ बहुत तेज़ी से घटता है और <math> x</math> के <math> 0</math> की ओर बढ़ने पर <math> -\infty</math> की ओर बढ़ता है। जब <math> x</math>, <math> +\infty</math> की ओर बढ़ता है, तो फलन भी लगातार घटती हुई वृद्धि दर के साथ <math> +\infty</math> की ओर बढ़ता है। फलन का सामान्य आलेख इस तरह दिखता है – (जहाँ <math> b = 2</math>) | |||
स्थिति 2: <math> 0 < b < 1</math> | |||
[[File:लघुगणकीय फलन-2.jpg|thumb|लघुगणकीय फलन-2]] | |||
यहाँ <math> x</math> के <math> 0</math> की ओर बढ़ने पर फलन बहुत तेज़ी से <math> +\infty</math> तक बढ़ता है, और <math> x</math> के <math> +\infty</math> की ओर बढ़ने पर लगातार घटती दर से <math> -\infty</math> तक गिरता है। सामान्य आलेख इस प्रकार दिखाया गया है - (जहाँ <math> b = 0.5</math> | |||
== लघुगणकीय फलनों के गुण == | |||
b | * लघुगणकीय फलन का प्रांत <math>(0,+\infty)</math> है। | ||
* लघुगणकीय फलन की सीमा <math>(-\infty,+\infty)</math> है। | |||
* बिंदु <math>(1,0)</math> और <math>(b,1)</math> सदैव फलन <math> \log_{b}x</math> के आलेख पर स्थित होते हैं। | |||
* गुणनफल नियम – | |||
<math> \log_{b}(xy)= \log_{b}x+ \log_{b}y</math> | |||
* भागफल नियम – | |||
<math> \log_{b}(\frac{x}{y})= \log_{b}x- \log_{b}y</math> | |||
* घात नियम: | |||
<math> \log_{b}a^x=x \log_{b}a</math> | |||
सामान्यीकरण: | |||
<math> \log_{b}a^{f(x)}=f(x) \log_{b}a</math> | |||
* आधार सूत्र का परिवर्तन – किसी दिए गए आधार ‘<math> b</math>’ से आधार ‘<math> a</math>’ तक लघुगणक को परिवर्तित करना। | |||
<math> \log_{b}x=\frac{\log_{a}x}{\log_{a}b}</math> | |||
* लघुगणकीय फलन अपने पूरे प्रांत में निरंतर और अवकलनीय है। अवकलज इस प्रकार दिया गया है। | |||
<math> {d(\log_{b}x) \over dx} =\frac{1}{x\ln(b)}</math> | |||
जहाँ <math> \ln(b)</math> या <math> log_eb, b</math> का प्राकृतिक लघुगणक है। यह एक मानक लघुगणक फलन है। इसका आधार <math> = e = 2.71828</math>है। इसका अवकलज - | |||
<math> {d(\ln(x)) \over dx}=\frac{1}{x}</math> | |||
– चूँकि <math> \ln(e) = 1</math> । | |||
== चरघातांकी और लघुगणकीय फलनों के बीच संबंध == | |||
हम आपको पहले ही बता चुके हैं कि लघुगणक और चरघातांकी फलन एक दूसरे के व्युत्क्रम हैं। अब आप गुणों से भी इसकी पुष्टि कर सकते हैं। | |||
* दोनों फलनों की सीमा और प्रांत का आदान-प्रदान किया जाता है। | |||
* बिंदु <math>(0,1)</math>और <math>(1, a)</math> सदैव चरघातांकी फलन के आलेख पर स्थित होते हैं जबकि<math>(1,0)</math> और <math>(b,1)</math> सदैव लघुगणकीय फलन के आलेख पर स्थित होते हैं। | |||
* चरघातांकी और लघुगणक फलनों के गुणनफल और भागफल नियम एक दूसरे से अनुसरण करते हैं। | |||
आइए अब हम अपने कथन को मानक फलनों के लिए गणितीय रूप में प्रस्तुत करें – | |||
<math> e^{\ln(x)}=\ln(e^x)=x</math> | |||
सामान्य सूत्र – | |||
== चरघातांकी | <math> b^{\log_{b}x}=\log_{b}b^x=x | ||
</math> | |||
[[File:चरघातांकी तथा लघूगणकीय फलन.jpg|thumb|चरघातांकी तथा लघूगणकीय फलन]] | |||
== उदाहरण == | |||
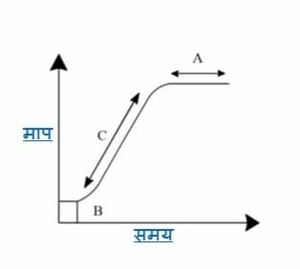
प्रश्न: नीचे वृध्दि बनाम समय के मापदंडों पर बनाया गया एक आलेख दिया गया है। A, B, C क्रमशः दर्शाते हैं | |||
चरघातांकी और | * चरघातांकी चरण, लघुगणकीय चरण और स्थायी अवस्था चरण | ||
* स्थायी अवस्था चरण, पश्चता प्रावस्था चरण और लघुगणकीय चरण | |||
* धीमी गति से बढ़ने वाला चरण, पश्चता प्रावस्था चरण और स्थायी अवस्था चरण | |||
* पश्चता प्रावस्था चरण, स्थायी अवस्था चरण और लघुगणकीय चरण | |||
* लघुगणकीय चरण, पश्चता प्रावस्था चरण और स्थायी अवस्था चरण | |||
समाधान: <math> B</math> वृध्दि चरण में पहला चरण पश्चता प्रावस्थाचरण होता है, जहाँ न्यूनतम वृद्धि होती है। वृद्धि चरण में अगला चरण लघुगणकीय चरण होता है, जिसे चरघातांकी चरण के रूप में भी जाना जाता है जहाँ वृद्धि कई गुना होती है। अंतिम चरण एक स्थायी अवस्था होती है जहाँ वृद्धि शून्य होती है और इस प्रकार इसे स्थायी अवस्था के रूप में जाना जाता है। | |||
यह चरघातांकी और लघुगणकीय फलनों के इस विषय पर हमारी चर्चा का समापन करता है। | |||
[[Category:सांतत्य तथा अवकलनीयता]][[Category:गणित]][[Category:कक्षा-12]] | [[Category:सांतत्य तथा अवकलनीयता]][[Category:गणित]][[Category:कक्षा-12]] | ||
Latest revision as of 08:25, 2 December 2024
चरघातांकी और लघुगणकीय फलन संभवतः सबसे महत्वपूर्ण फलन हैं जिनका सामना आपको किसी भौतिक समस्या से निपटने के दौरान करना होगा। वे एक दूसरे के व्युत्क्रम या प्रतिलोम हैं और संख्याओं की एक बड़ी श्रृंखला को बहुत आसानी से दर्शाने के लिए उपयोग किया जा सकता है।
वे अपने पूरे प्रांत में सांतत्य और अवकलनीय हैं, और उनके अवकलजों के संकेतन में सरलता, आपको गणित के साथ-साथ अन्य विषयों में उनके विशाल महत्व के बारे में एक विचार देगी। आइए अब हम इन फलनों को व्यक्तिगत रूप से समझते हैं, उनके बीच संबंध पर आगे बढ़ने से पहले।
चरघातांकी फलन
'घातांक' शब्द का तात्पर्य किसी संख्या की 'घात' से है। उदाहरण के लिए - संख्या में 2 का घातांक 3 के बराबर है। स्पष्ट रूप से, चरघातांकी फलन वे होते हैं जहाँ चर घात के रूप में होता है। चरघातांकी फलन को इस प्रकार परिभाषित किया जाता है-
जहाँ एक धनात्मक वास्तविक संख्या है, जो के बराबर नहीं है।
यदि तो जो , के बराबर है। इसलिए फलन का आलेख स्थिरांक की एक सरल रेखा होगी। ‘’ के मान के आधार पर, हमारे पास दो संभावित स्थितियाँ हो सकते हैं:
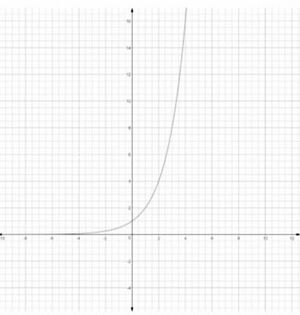
स्थिति 1:
यहाँ, चरघातांकी फलन के बढ़ने के साथ बहुत तेज़ी से बढ़ता है और के की ओर बढ़ने पर की ओर बढ़ता है। जब और जब , की ओर बढ़ता है, तो फलन की ओर बढ़ता है। फलन का सामान्य आलेख इस तरह दिखता है: (जहाँ )
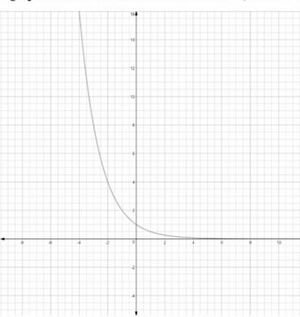
स्थिति 2:
फलन के बढ़ने के साथ बहुत तेज़ी से घटता है और के की ओर बढ़ने पर की ओर बढ़ता है। जब सदैव की तरह; और जब , की ओर बढ़ता है, तो फलन की ओर बढ़ता है। ऐसे फलन का सामान्य आलेख इस तरह दिखता है - (जहाँ फिर से)
चरघातांकी फलनों के गुण
- चरघातांकी फलन का प्रांत है, अर्थात इसे से परिभाषित किया जाता है।
- चरघातांकी फलन की सीमा है। यह गुण फलन के आलेख से स्पष्ट होना चाहिए। अन्यथा, यह भी तर्कसंगत है कि किसी भी वास्तविक संख्या की घात ऋणात्मक संख्या नहीं हो सकती। मात्र काल्पनिक संख्याओं में ही ऐसा व्यवहार हो सकता है।
- बिंदु और सदैव फलन के आलेख पर स्थित होते हैं।
- ‘’ अनिवार्य रूप से एक धनात्मक संख्या होनी चाहिए। यदि एक ऋणात्मक संख्या है, तो के किसी भी भिन्नात्मक मान के लिए, हमें परिणाम के रूप में एक काल्पनिक संख्या मिलेगी जिसे उसी आलेख पर आलेखित नहीं किया जा सकता है। उदाहरण के लिए-
- गुणनफल नियम –
- भागफल नियम –
- चरघातांकी फलन अपने पूरे प्रांत में संतत और अवकलनीय है। अवकलज इस प्रकार दिया गया है
जहाँ या का प्राकृतिक लघुगणक है। हम इसे कुछ समय में औपचारिक रूप से परिभाषित करेंगे। मानक चरघातांकी फलन गणित में एक अद्वितीय फलन है जिसमें इसके अवकलज के बराबर होने का गुण होता है। इस प्रकार, हमारे पास है
वास्तव में, इन अवकलजों के पीछे की गणना संख्या ‘’ को परिभाषित करने के तरीकों में से एक है जो के बराबर है… अभी के लिए चरघातांकी फलनों के बारे में इतना ही।
लघुगणकीय फलन
चूँकि हमने पहले ही उजागर कर दिया था कि लघुगणक फलन और चरघातांकी फलन एक दूसरे के प्रतिलोम हैं, इसलिए यह स्पष्ट होना चाहिए कि लघुगणक फलन ‘किसी संख्या की घात लेने’ के विपरीत फलन करता है। आइए इसे गणितीय रूप से देखें –
सामान्य संकेतन
- घातांकीय रूप –
- लघुगणकीय रूप –
जहाँ ‘’ लघुगणक का आधार है।
इन दो रूपों के साथ, आप आसानी से देख सकते हैं कि फलन का मान वह घात है जिस तक ‘’ को बढ़ाकर ‘’ प्राप्त करना होगा। इसलिए, ‘’ ऋणात्मक नहीं हो सकता क्योंकि इसके लिए ‘’ को काल्पनिक होना आवश्यक है, आधार ‘’ पर स्थितियाँ –
- : यह लघूगणकीय फलन के चरघातांकी निरूपण से सीधे अनुसरण करता है।
- : चूँकि 1 को किसी भी घात तक बढ़ाने पर केवल 1 ही प्राप्त होगा।
‘’ के मान के आधार पर, हमारे पास दो संभावित मामले होंगे –
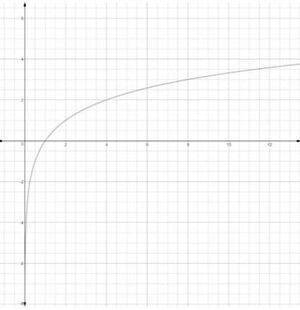
स्थिति 1:
यहाँ, लघूगणकीय फलन के घटने के साथ बहुत तेज़ी से घटता है और के की ओर बढ़ने पर की ओर बढ़ता है। जब , की ओर बढ़ता है, तो फलन भी लगातार घटती हुई वृद्धि दर के साथ की ओर बढ़ता है। फलन का सामान्य आलेख इस तरह दिखता है – (जहाँ )
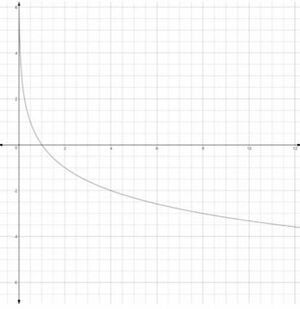
स्थिति 2:
यहाँ के की ओर बढ़ने पर फलन बहुत तेज़ी से तक बढ़ता है, और के की ओर बढ़ने पर लगातार घटती दर से तक गिरता है। सामान्य आलेख इस प्रकार दिखाया गया है - (जहाँ
लघुगणकीय फलनों के गुण
- लघुगणकीय फलन का प्रांत है।
- लघुगणकीय फलन की सीमा है।
- बिंदु और सदैव फलन के आलेख पर स्थित होते हैं।
- गुणनफल नियम –
- भागफल नियम –
- घात नियम:
सामान्यीकरण:
- आधार सूत्र का परिवर्तन – किसी दिए गए आधार ‘’ से आधार ‘’ तक लघुगणक को परिवर्तित करना।
- लघुगणकीय फलन अपने पूरे प्रांत में निरंतर और अवकलनीय है। अवकलज इस प्रकार दिया गया है।
जहाँ या का प्राकृतिक लघुगणक है। यह एक मानक लघुगणक फलन है। इसका आधार है। इसका अवकलज -
– चूँकि ।
चरघातांकी और लघुगणकीय फलनों के बीच संबंध
हम आपको पहले ही बता चुके हैं कि लघुगणक और चरघातांकी फलन एक दूसरे के व्युत्क्रम हैं। अब आप गुणों से भी इसकी पुष्टि कर सकते हैं।
- दोनों फलनों की सीमा और प्रांत का आदान-प्रदान किया जाता है।
- बिंदु और सदैव चरघातांकी फलन के आलेख पर स्थित होते हैं जबकि और सदैव लघुगणकीय फलन के आलेख पर स्थित होते हैं।
- चरघातांकी और लघुगणक फलनों के गुणनफल और भागफल नियम एक दूसरे से अनुसरण करते हैं।
आइए अब हम अपने कथन को मानक फलनों के लिए गणितीय रूप में प्रस्तुत करें –
सामान्य सूत्र –
उदाहरण
प्रश्न: नीचे वृध्दि बनाम समय के मापदंडों पर बनाया गया एक आलेख दिया गया है। A, B, C क्रमशः दर्शाते हैं
- चरघातांकी चरण, लघुगणकीय चरण और स्थायी अवस्था चरण
- स्थायी अवस्था चरण, पश्चता प्रावस्था चरण और लघुगणकीय चरण
- धीमी गति से बढ़ने वाला चरण, पश्चता प्रावस्था चरण और स्थायी अवस्था चरण
- पश्चता प्रावस्था चरण, स्थायी अवस्था चरण और लघुगणकीय चरण
- लघुगणकीय चरण, पश्चता प्रावस्था चरण और स्थायी अवस्था चरण
समाधान: वृध्दि चरण में पहला चरण पश्चता प्रावस्थाचरण होता है, जहाँ न्यूनतम वृद्धि होती है। वृद्धि चरण में अगला चरण लघुगणकीय चरण होता है, जिसे चरघातांकी चरण के रूप में भी जाना जाता है जहाँ वृद्धि कई गुना होती है। अंतिम चरण एक स्थायी अवस्था होती है जहाँ वृद्धि शून्य होती है और इस प्रकार इसे स्थायी अवस्था के रूप में जाना जाता है।
यह चरघातांकी और लघुगणकीय फलनों के इस विषय पर हमारी चर्चा का समापन करता है।