समाकलन की विधियाँ: Difference between revisions
(formulas) |
No edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
समाकलन, एक संपूर्ण को ज्ञात करने के लिए भाग को एकजुट करने का एक उपाय है। समाकलन कलन में, हम एक ऐसा फलन पाते हैं जिसका अंतर दिया गया है। इस प्रकार समाकलन [[अवकलनीयता|अवकलन]] का प्रतिलोम है। समाकलन का उपयोग फलन के आलेख द्वारा परिबद्ध क्षेत्र के क्षेत्र को परिभाषित करने और गणना करने के लिए किया जाता है। वक्र आकार का क्षेत्र इसमें अंकित बहुभुज की भुजाओं की संख्या को ज्ञात कर अनुमानित किया जाता है। निःशेषण(क्सहॉशन) की विधि के रूप में जानी जाने वाली इस प्रक्रिया को बाद में समाकलन के रूप में अपनाया गया। | |||
== परिचय == | == परिचय == | ||
हम समाकल के दो रूप प्राप्त करते हैं, '''अनिश्चित''' और '''निश्चित''' समाकल। अवकलन और समाकलन कलन में मौलिक उपकरण हैं जिनका उपयोग गणित और भौतिकी में समस्याओं को हल करने के लिए किया जाता है। समाकलन के सिद्धांत लाइबनिज द्वारा तैयार किए गए थे। आइए आगे बढ़ते हैं और समाकलन , इसके गुणों और इसकी कुछ शक्तिशाली तकनीकों के बारे में सीखते हैं। | हम समाकल के दो रूप प्राप्त करते हैं, '''अनिश्चित''' और '''निश्चित''' समाकल। अवकलन और समाकलन कलन में मौलिक उपकरण हैं जिनका उपयोग गणित और भौतिकी में समस्याओं को हल करने के लिए किया जाता है। समाकलन के सिद्धांत लाइबनिज द्वारा तैयार किए गए थे। आइए आगे बढ़ते हैं और समाकलन , इसके गुणों और इसकी कुछ शक्तिशाली तकनीकों के बारे में सीखते हैं। | ||
| Line 8: | Line 8: | ||
== समाकलन के उपाय == | == समाकलन के उपाय == | ||
कभी-कभी, कुछ फलन का | कभी-कभी, कुछ फलन का समाकलन ज्ञात करने के लिए निरीक्षण पर्याप्त नहीं होता है। इसके समाकलन को ज्ञात करने के लिए मानक रूप में फलन को कम करने के लिए अतिरिक्त तरीके हैं। प्रमुख तरीकों पर नीचे चर्चा की गई है। | ||
समाकलन के तरीके हैं: | समाकलन के तरीके हैं: | ||
| Line 31: | Line 31: | ||
=== विधि 2: प्रतिस्थापन द्वारा समाकलन === | === विधि 2: प्रतिस्थापन द्वारा समाकलन === | ||
प्रतिस्थापन द्वारा समाकलन विधि हमें समाकलन के चर को बदलने देती है ताकि समाकलन को आसान तरीके से एकीकृत किया जा सके।<math>mx = t</math> | प्रतिस्थापन द्वारा समाकलन विधि हमें समाकलन के चर को बदलने देती है ताकि समाकलन को आसान तरीके से एकीकृत किया जा सके। <math>mx = t</math> | ||
मान लीजिए, हमें <math>y =\int f(x) dx</math> ज्ञात करना है। | मान लीजिए, हमें <math>y =\int f(x) dx</math> ज्ञात करना है। | ||
| Line 64: | Line 64: | ||
=== विधि 3: आंशिक भिन्नों का उपयोग करके समाकलन === | === विधि 3: आंशिक भिन्नों का उपयोग करके समाकलन === | ||
मान लीजिए हमें y= | मान लीजिए हमें <math>y={P(x) \over Q(x)}dx</math> ज्ञात करना है, जहाँ <math>{P(x) \over Q(x)}</math> एक अनुचित परिमेय फलन है। हम इसे इस तरह से घटाते हैं कि <math>{P(x) \over Q(x)}=T(x)+ {P_1(x) \over Q(x)}</math> । यहाँ, <math>T(x)</math>, <math>x</math> में बहुपद है और <math>{P_1(x) \over Q(x)}</math> उचित परिमेय फलन है। | ||
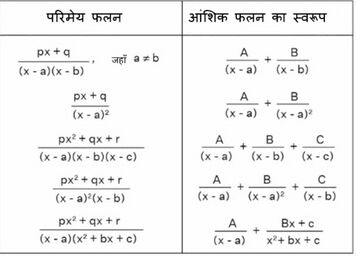
निम्न तालिका कुछ परिमेय फलनों और आंशिक भिन्नों के उनके संगत रूप को दर्शाती है।[[File:आंशिक भिन्नों द्वारा समाकलन.jpg|thumb|356x356px|आंशिक भिन्नों द्वारा समाकलन]] | |||
उदाहरण के लिए, आइए इसका समाकल ज्ञात करें | |||
<math>f(x)=\frac{1}{(x+1)(x+2)}</math> आंशिक अंशों द्वारा एकीकरण का उपयोग करना। | |||
आंशिक भिन्न का उपयोग करने पर हमें यह प्राप्त होता है <math>\frac{1}{(x+1)(x+2)} =\frac{A}{x+1}+\frac{B}{x+2}...1)</math> | |||
हम <math>A</math> और <math>B</math> के मान निर्धारित करेंगे। | |||
समीकरण (1) की तुलना करने पर, हमें <math>1=A(x+2)+B(x+1)</math> प्राप्त होता है | |||
इससे हमें दो रैखिक समीकरणों का एक समूह प्राप्त होता है। | |||
<math>A+B=0</math> और <math>2A+B =1</math> | |||
इन समीकरणों को हल करने पर, <math>A=1</math>और <math>B=-1</math> प्राप्त होता है। | |||
इसलिए, समीकरण (1) को <math>\frac{1}{(x+1)(x+2)}=\frac{1}{x+1}-\frac{1}{x+2}</math> के रूप में लिखा जा सकता है। | |||
अब, समाकलन को हल करते हुए | |||
<math>\int (\frac{1}{(x+1)(x+2)})dx</math> | |||
<math>=\int (\frac{1}{x+1}- \frac{1}{x+2})dx</math> | |||
<math>=\log \left\vert x+1 \right\vert - \log \left\vert x+2 \right\vert + C</math> | |||
<math>= \log \left\vert \frac{x+1}{x+2} \right\vert + C</math> | |||
=== विधि 4: खंडशः समाकलन === | |||
इस समाकलन नियम का उपयोग दो फलनों का अभिन्न समाकलन ज्ञात करने के लिए किया जाता है। | |||
अवकलाजों के गुणन नियम से, हमारे पास है <math>{d(uv) \over dx}=u{dv \over dx}+v{du \over dx}...1)</math> | |||
= | समीकरण (1) के दोनों पक्षों पर समाकलन, हमें मिलता है <math>\int u {dv \over dx}dx =uv - \int v\ {du \over dx}dx...2)</math> | ||
समीकरण (2) को इस प्रकार लिखा जा सकता है <math>uv=\int u {dv \over dx}dx+\int v{du \over dx}dx</math> | |||
मान लीजिए <math>u=f(x)</math> और <math>{dv \over dx}=g(x)</math> | |||
तो, हमारे पास है <math>{du \over dx}=f'(x)</math> और <math>v = \int g(x)dx</math> | |||
तो, समीकरण (2) बन जाता है | |||
<math>\int f(x)g(x)dx</math> | |||
<math>=f(x)\int g(x)dx-\int [f'(x) \int g(x)dx]dx</math> | |||
उदाहरण के लिए, आइए भागों द्वारा एकीकरण का उपयोग करके <math>xe^x</math> का समाकल ज्ञात करें। | |||
<math>\int xe^xdx=x\int e^xdx-\int ({dx \over dx}\int e^xdx]dx</math> | |||
<math>=xe^x-\int [e^x)dx</math> | |||
<math>=xe^x-e^x+C</math> | |||
कुछ महत्वपूर्ण मानक परिणाम (बर्नौली का सूत्र): | |||
* <math>\int e^{ax} sin\ bx\ dx = e^{ax} /(a^2 + b^2)[a\ sin\ bx - b\ cos\ bx] + C</math> | |||
* <math>\int e^{ax} cos\ bx\ dx = e^{ax} /(a^2 + b^2)[a\ cos\ bx + b\ sin\ bx] + C</math> | |||
[[Category:समाकलन]][[Category:गणित]][[Category:कक्षा-12]] | [[Category:समाकलन]][[Category:गणित]][[Category:कक्षा-12]] | ||
Latest revision as of 10:35, 5 December 2024
समाकलन, एक संपूर्ण को ज्ञात करने के लिए भाग को एकजुट करने का एक उपाय है। समाकलन कलन में, हम एक ऐसा फलन पाते हैं जिसका अंतर दिया गया है। इस प्रकार समाकलन अवकलन का प्रतिलोम है। समाकलन का उपयोग फलन के आलेख द्वारा परिबद्ध क्षेत्र के क्षेत्र को परिभाषित करने और गणना करने के लिए किया जाता है। वक्र आकार का क्षेत्र इसमें अंकित बहुभुज की भुजाओं की संख्या को ज्ञात कर अनुमानित किया जाता है। निःशेषण(क्सहॉशन) की विधि के रूप में जानी जाने वाली इस प्रक्रिया को बाद में समाकलन के रूप में अपनाया गया।
परिचय
हम समाकल के दो रूप प्राप्त करते हैं, अनिश्चित और निश्चित समाकल। अवकलन और समाकलन कलन में मौलिक उपकरण हैं जिनका उपयोग गणित और भौतिकी में समस्याओं को हल करने के लिए किया जाता है। समाकलन के सिद्धांत लाइबनिज द्वारा तैयार किए गए थे। आइए आगे बढ़ते हैं और समाकलन , इसके गुणों और इसकी कुछ शक्तिशाली तकनीकों के बारे में सीखते हैं।
समाकलन वक्र के नीचे के क्षेत्र का क्षेत्रफल ज्ञात करने की प्रक्रिया है। यह क्षेत्र को आवरण करने वाले जितने भी छोटे आयत हों, उन्हें खींचकर और उनके क्षेत्रों को जोड़कर किया जाता है। योग एक सीमा के निकट पहुंचता है जो फलन के वक्र के नीचे के क्षेत्र के समान होता है। समाकलन फलन के प्रति अवकलज को ज्ञात करने की प्रक्रिया है। यदि कोई फलन समाकलनीय है और यदि प्रांत पर उसका समाकलन परिमित है, जिसकी सीमाएँ निर्दिष्ट हैं, तो यह निश्चित समाकलन है।
समाकलन के उपाय
कभी-कभी, कुछ फलन का समाकलन ज्ञात करने के लिए निरीक्षण पर्याप्त नहीं होता है। इसके समाकलन को ज्ञात करने के लिए मानक रूप में फलन को कम करने के लिए अतिरिक्त तरीके हैं। प्रमुख तरीकों पर नीचे चर्चा की गई है।
समाकलन के तरीके हैं:
- अपघटित विधि
- प्रतिस्थापन द्वारा समाकलन
- आंशिक भिन्नों द्वारा समाकलन
- खंडशः समाकलन
विधि 1: अपघटित विधि द्वारा समाकलन
फलन को ऐसे फलन के योग या अंतर में अपघटित किया जा सकता है, जिनके व्यक्तिगत समाकलन ज्ञात हैं। दिया गया समाकलन बीजीय, त्रिकोणमितीय या घातांकीय या इन फलनों का संयोजन होगा।
मान लीजिए हमें को एकीकृत करने की आवश्यकता है, तो हम फलन को इस प्रकार अपघटित करते हैं:
व्युत्क्रम नियम और घात नियम लागू करने पर, हम प्राप्त होता हैं
विधि 2: प्रतिस्थापन द्वारा समाकलन
प्रतिस्थापन द्वारा समाकलन विधि हमें समाकलन के चर को बदलने देती है ताकि समाकलन को आसान तरीके से एकीकृत किया जा सके।
मान लीजिए, हमें ज्ञात करना है।
मान लीजिए । फिर,
तो, को के रूप में लिखा जा सकता है।
उदाहरण के लिए, प्रतिस्थापन का उपयोग करके का समाकल ज्ञात करें।
मान लीजिए । फिर,
को के रूप में लिखा जा सकता है
ध्यान दें: समाकलन के चर के प्रतिस्थापन में त्रिकोणमितीय पहचान का भी उपयोग किया जा सकता है। कुछ महत्वपूर्ण मानक परिणाम इस प्रकार हैं:
विधि 3: आंशिक भिन्नों का उपयोग करके समाकलन
मान लीजिए हमें ज्ञात करना है, जहाँ एक अनुचित परिमेय फलन है। हम इसे इस तरह से घटाते हैं कि । यहाँ, , में बहुपद है और उचित परिमेय फलन है।
निम्न तालिका कुछ परिमेय फलनों और आंशिक भिन्नों के उनके संगत रूप को दर्शाती है।
उदाहरण के लिए, आइए इसका समाकल ज्ञात करें
आंशिक अंशों द्वारा एकीकरण का उपयोग करना।
आंशिक भिन्न का उपयोग करने पर हमें यह प्राप्त होता है
हम और के मान निर्धारित करेंगे।
समीकरण (1) की तुलना करने पर, हमें प्राप्त होता है
इससे हमें दो रैखिक समीकरणों का एक समूह प्राप्त होता है।
और
इन समीकरणों को हल करने पर, और प्राप्त होता है।
इसलिए, समीकरण (1) को के रूप में लिखा जा सकता है।
अब, समाकलन को हल करते हुए
विधि 4: खंडशः समाकलन
इस समाकलन नियम का उपयोग दो फलनों का अभिन्न समाकलन ज्ञात करने के लिए किया जाता है।
अवकलाजों के गुणन नियम से, हमारे पास है
समीकरण (1) के दोनों पक्षों पर समाकलन, हमें मिलता है
समीकरण (2) को इस प्रकार लिखा जा सकता है
मान लीजिए और
तो, हमारे पास है और
तो, समीकरण (2) बन जाता है
उदाहरण के लिए, आइए भागों द्वारा एकीकरण का उपयोग करके का समाकल ज्ञात करें।
कुछ महत्वपूर्ण मानक परिणाम (बर्नौली का सूत्र):