सप्रतिबंध प्रायिकता: Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 3: | Line 3: | ||
आइए सप्रतिबंध प्रायिकता के बारे में इसके सूत्र, उदाहरणों और अभ्यास प्रश्नों के साथ और अधिक जानें। | आइए सप्रतिबंध प्रायिकता के बारे में इसके सूत्र, उदाहरणों और अभ्यास प्रश्नों के साथ और अधिक जानें। | ||
सप्रतिबंध प्रायिकता | सप्रतिबंध प्रायिकता, [[प्रायिकता का सांख्यिकीय दृष्टिकोण|प्रायिकता]] और [[सांख्यिकी]] में महत्वपूर्ण अवधारणाओं में से एक है। "<math>B</math> दिए जाने पर <math>A</math> की प्रायिकता " (या) "स्थिति <math>B</math> के संबंध में <math>A</math> की प्रायिकता " को सप्रतिबंध प्रायिकता <math>P(A | B)</math> (या) <math>P (A / B)</math> (या) <math>P_B (A)</math> द्वारा दर्शाया जाता है। इस प्रकार, <math>P(A | B)</math>, <math>A</math> की प्रायिकता को दर्शाता है जो घटना <math>B</math> के पहले ही घटित हो जाने के बाद घटित होती है। यदि कोई शर्त दी गई हो तो किसी घटना की प्रायिकता बदल सकती है। | ||
== परिभाषा == | == परिभाषा == | ||
| Line 11: | Line 11: | ||
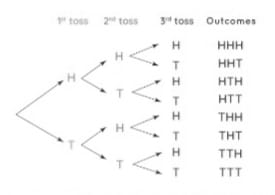
आइए एक उदाहरण के साथ सप्रतिबंध प्रायिकता को समझें। आइए कम से कम दो पट प्राप्त करने की सप्रतिबंध प्रायिकता का पता लगाएं, यह देखते हुए कि जब 3 सिक्के उछाले जाते हैं तो पहली सिक्का उछालना पर चित आता है। नमूना स्थान, <math>S</math> (सभी परिणामों की सूची) जब 3 सिक्के उछाले जाते हैं, तो निम्नानुसार दिया गया है: | आइए एक उदाहरण के साथ सप्रतिबंध प्रायिकता को समझें। आइए कम से कम दो पट प्राप्त करने की सप्रतिबंध प्रायिकता का पता लगाएं, यह देखते हुए कि जब 3 सिक्के उछाले जाते हैं तो पहली सिक्का उछालना पर चित आता है। नमूना स्थान, <math>S</math> (सभी परिणामों की सूची) जब 3 सिक्के उछाले जाते हैं, तो निम्नानुसार दिया गया है: | ||
आइए हम दो घटनाओं <math>A</math> और <math>B</math> को इस प्रकार मानें: | आइए हम दो [[स्वतंत्र घटनाएँ|घटनाओं]] <math>A</math> और <math>B</math> को इस प्रकार मानें: | ||
<math>A =</math> कम से कम दो पट आने की घटना | <math>A =</math> कम से कम दो पट आने की घटना | ||
| Line 31: | Line 31: | ||
इसी तरह, हम <math>P(B | A)</math> को इस प्रकार परिभाषित कर सकते हैं: | इसी तरह, हम <math>P(B | A)</math> को इस प्रकार परिभाषित कर सकते हैं: | ||
<math>P(B | A) = P(A \cap B) / P(A)</math> (ध्यान दें कि यहाँ <math>P(A) \neq 0</math> है) | <math>P(B | A) = P(A \cap B) / P(A)</math> (ध्यान दें कि यहाँ <math>P(A) \neq 0</math> है) | ||
इन सूत्रों को सप्रतिबंध संभाव्यता की "कोल्मोगोरोव परिभाषा" के रूप में भी जाना जाता है। | इन सूत्रों को सप्रतिबंध संभाव्यता की "कोल्मोगोरोव परिभाषा" के रूप में भी जाना जाता है। | ||
| Line 43: | Line 43: | ||
* <math>P(B) = B</math> की प्रायिकता | * <math>P(B) = B</math> की प्रायिकता | ||
== सप्रतिबंध | == सप्रतिबंध प्रायिकता की व्युत्पत्ति == | ||
ध्यान दें कि <math>B</math> के वे तत्व जो घटना <math>A</math> के पक्ष में हैं, <math>A</math> और <math>B</math> के सामान्य तत्व हैं। यानी <math>A \cap B</math> के नमूना बिंदु। | ध्यान दें कि <math>B</math> के वे तत्व जो घटना <math>A</math> के पक्ष में हैं, <math>A</math> और <math>B</math> के सामान्य तत्व हैं। यानी <math>A \cap B</math> के नमूना बिंदु। | ||
| Line 56: | Line 56: | ||
=== गुणधर्म 1 === | === गुणधर्म 1 === | ||
मान लीजिए कि S किसी प्रयोग का नमूना स्थान है और <math>A</math> कोई भी घटना है। फिर | मान लीजिए कि <math>S</math> किसी प्रयोग का नमूना स्थान है और <math>A</math> कोई भी घटना है। फिर | ||
<math>P(S | A) = P(A | A) = 1</math> | <math>P(S | A) = P(A | A) = 1</math> | ||
| Line 94: | Line 94: | ||
प्रमाण''':''' | प्रमाण''':''' | ||
गुणधर्म 1 से, हमारे पास है <math>P(S | B) = 1</math> | |||
हम जानते हैं कि <math>S = A \cup A'</math> इस प्रकार उपरोक्त गुणधर्म से, | |||
P( A | <math>P( A \cup A' | B) = 1</math> | ||
चूँकि <math>A</math> और <math>A'</math> असंयुक्त घटनाएँ हैं, | |||
P(A | B) + P(A' | B) = 1 | <math>P(A | B) + P(A' | B) = 1</math> | ||
P(A' | B) = 1 - P(A | B) | <math>P(A' | B) = 1 - P(A | B)</math> | ||
अतः गुणधर्म 3 सिद्ध है। | अतः गुणधर्म 3 सिद्ध है। | ||
Latest revision as of 13:27, 18 December 2024
सप्रतिबंध प्रायिकता , जैसा कि इसके नाम से पता चलता है, किसी घटना के घटित होने की प्रायिकता है जो किसी शर्त पर आधारित होती है। उदाहरण के लिए, मान लें कि शाम को टेनिस खेलने वाले लड़के की प्रायिकता है जबकि बारिश के दिन होने पर उसके खेलने की प्रायिकता कम है जो कि है। तो पहला मामला सामान्य प्रायिकता है जबकि दूसरा मामला सप्रतिबंध प्रायिकता है। इस उदाहरण में, हम दो प्रायिकता ओं को (टेनिस खेलें) और (टेनिस खेलें | बरसात का दिन) के रूप में दर्शाते हैं।
आइए सप्रतिबंध प्रायिकता के बारे में इसके सूत्र, उदाहरणों और अभ्यास प्रश्नों के साथ और अधिक जानें।
सप्रतिबंध प्रायिकता, प्रायिकता और सांख्यिकी में महत्वपूर्ण अवधारणाओं में से एक है। " दिए जाने पर की प्रायिकता " (या) "स्थिति के संबंध में की प्रायिकता " को सप्रतिबंध प्रायिकता (या) (या) द्वारा दर्शाया जाता है। इस प्रकार, , की प्रायिकता को दर्शाता है जो घटना के पहले ही घटित हो जाने के बाद घटित होती है। यदि कोई शर्त दी गई हो तो किसी घटना की प्रायिकता बदल सकती है।
परिभाषा
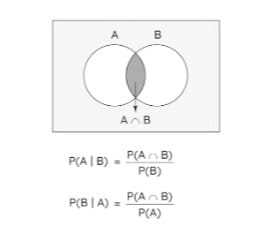
यदि और एक यादृच्छिक प्रयोग के एक ही नमूना स्थान से जुड़ी दो घटनाएँ हैं, तो घटना A की सप्रतिबंध प्रायिकता यह देखते हुए कि घटित हुई है, द्वारा दी जाती है, बशर्ते हो।
आइए एक उदाहरण के साथ सप्रतिबंध प्रायिकता को समझें। आइए कम से कम दो पट प्राप्त करने की सप्रतिबंध प्रायिकता का पता लगाएं, यह देखते हुए कि जब 3 सिक्के उछाले जाते हैं तो पहली सिक्का उछालना पर चित आता है। नमूना स्थान, (सभी परिणामों की सूची) जब 3 सिक्के उछाले जाते हैं, तो निम्नानुसार दिया गया है:
आइए हम दो घटनाओं और को इस प्रकार मानें:
कम से कम दो पट आने की घटना
पहले सिक्का उछालने पर चित आने की घटना
फिर और
फिर और
हमें कम से कम दो पट आने की प्रायिकता ज्ञात करनी है, बशर्ते कि पहला सिक्का उछालना पर चित आए. इसका मतलब है कि के सभी तत्वों में से हमें केवल दो पट वाले तत्वों को चुनना है. हम देख सकते हैं कि के तत्वों में से केवल एक तत्व (जो HTT है) है, जिसमें दो पट हैं. इस प्रकार, अपेक्षित प्रायिकता ( के 4 परिणामों में से का केवल 1 परिणाम के अनुकूल है) है.
सप्रतिबंध प्रायिकता सूत्र
उपर्युक्त उदाहरण में, हमें मिला है, यहाँ 1 तत्व HTT को दर्शाता है जो " और " दोनों में मौजूद है और में तत्वों की कुल संख्या को दर्शाता है। इसका उपयोग करके, हम सप्रतिबंध संभाव्यता का सूत्र इस प्रकार प्राप्त कर सकते हैं।
(ध्यान दें कि यहाँ है)
इसी तरह, हम को इस प्रकार परिभाषित कर सकते हैं:
(ध्यान दें कि यहाँ है)
इन सूत्रों को सप्रतिबंध संभाव्यता की "कोल्मोगोरोव परिभाषा" के रूप में भी जाना जाता है।
यहाँ:
- की प्रायिकता दिए जाने पर (या) की प्रायिकता जो के बाद होती है
- की प्रायिकता दिए जाने पर (या) की प्रायिकता जो के बाद होती है
- और दोनों के होने की प्रायिकता
- की प्रायिकता
- की प्रायिकता
सप्रतिबंध प्रायिकता की व्युत्पत्ति
ध्यान दें कि के वे तत्व जो घटना के पक्ष में हैं, और के सामान्य तत्व हैं। यानी के नमूना बिंदु।
इस प्रकार के अनुकूल घटनाओं की संख्या के अनुकूल घटनाओं की संख्या।
इस प्रकार
सप्रतिबंध प्रायिकता के गुणधर्म
यहाँ सप्रतिबंध प्रायिकता के कुछ गुणधर्म और उनके प्रमाण (व्युत्पन्न) दिए गए हैं, जिनका उपयोग हमें समस्याओं को हल करते समय करना पड़ सकता है। ये सभी गुणधर्म सप्रतिबंध प्रायिकता सूत्र (जिसका उल्लेख पिछले अनुभाग में किया गया है) पर निर्भर करते हैं।
गुणधर्म 1
मान लीजिए कि किसी प्रयोग का नमूना स्थान है और कोई भी घटना है। फिर
प्रमाण:
सप्रतिबंध प्रायिकता के सूत्र द्वारा,
अतः गुणधर्म 1 सिद्ध है।
गुणधर्म 2
मान लीजिए कि किसी प्रयोग का नमूना स्थान है और और कोई दो घटनाएँ हैं। मान लीजिए कि E कोई अन्य घटना है जिससे है। तब
प्रमाण:
सप्रतिबंध प्रायिकता के सूत्र द्वारा,
(समुच्चय की एक गुणधर्म का उपयोग करना)
(प्रायिकता के योग सिद्धांत का उपयोग करना)
(सप्रतिबंध प्रायिकता सूत्र द्वारा)
अतः गुणधर्म 2 सिद्ध है।
गुणधर्म 3
जहाँ समुच्चय का पूरक है।
प्रमाण:
गुणधर्म 1 से, हमारे पास है
हम जानते हैं कि इस प्रकार उपरोक्त गुणधर्म से,
चूँकि और असंयुक्त घटनाएँ हैं,
अतः गुणधर्म 3 सिद्ध है।