आंशिक भिन्नों द्वारा समाकलन: Difference between revisions
(Updated Category) |
(added content) |
||
| Line 1: | Line 1: | ||
आंशिक भिन्नों द्वारा समाकलन एक ऐसी विधि है जिसका उपयोग किसी परिमेय भिन्न समाकलन को विघटित करने और फिर समाकलित करने के लिए किया जाता है जिसके हर में जटिल पद होते हैं। आंशिक भिन्न का उपयोग करके, हम व्यंजक की गणना करते हैं और उसे सरल पदों में विघटित करते हैं ताकि हम इस प्रकार प्राप्त व्यंजक की आसानी से गणना या एकीकरण कर सकें। | |||
आंशिक भिन्नों द्वारा समाकलन में मूल विचार हर को गुणनखंडित करना और फिर उन्हें दो अलग-अलग भिन्नों में विघटित करना है जहाँ हर क्रमशः गुणनखंड होते हैं और अंश की गणना उपयुक्त रूप से की जाती है। आइए आंशिक भिन्नों द्वारा समाकलन में उपयोग किए जाने वाले विभिन्न रूपों और विभिन्न विधियों के बारे में अधिक जानें। | |||
आंशिक भिन्नों द्वारा एकीकरण क्या है? | |||
आंशिक भिन्नों द्वारा एकीकरण एकीकरण की तीन विधियों में से एक है। इस विधि में, हम उचित परिमेय भिन्न को सरल परिमेय भिन्नों के योग में विघटित करते हैं। परिमेय भिन्न को सरल परिमेय भिन्नों में विघटित करना हमेशा संभव होता है और यह आंशिक भिन्न अपघटन नामक प्रक्रिया द्वारा किया जाता है। आइए इसे एक उदाहरण की मदद से समझते हैं। मान लीजिए हमारे पास 5/6 है, तो हम इसे 5/6 = 1/2 + 1/3 के रूप में विघटित कर सकते हैं, इसी तरह, हम दो आंशिक भिन्नों को बीजगणितीय रूप से विघटित करके ऐसा करते हैं। मान लीजिए हमारे पास है: | |||
2/(x+1) - 1/x | |||
on adding we will get | |||
2/(x+1) - 1/x = (x-1)/(x<sup>2</sup>+x). | |||
Now if we have | |||
(x-1)/(x<sup>2</sup>+x) | |||
so we can decompose it into | |||
(x-1)/(x<sup>2</sup>+x) = 2/(x+1) - 1/x | |||
इस प्रकार आंशिक भिन्नों को सरल पदों में विघटित कर दिया गया है। इसलिए अब परिणामी पदों को एकीकृत करना अपेक्षाकृत आसान कार्य होगा। आंशिक भिन्नों द्वारा एकीकरण इस प्रकार होगा: | |||
∫[f(x)/g(x)]dx = ∫[p(x)/q(x)]dx + ∫[r(x)/s(x)]dx | |||
where | |||
* f(x)/g(x) = p(x)/q(x) + r(x)/s(x) and | |||
* g(x) = q(x).s(x) | |||
आंशिक भिन्नों द्वारा समाकलन में प्रयुक्त रूप | |||
आंशिक भिन्नों द्वारा समाकलन में, हम उचित परिमेय भिन्नों के विशिष्ट रूपों को विघटित करने के लिए कुछ विशेष प्रकार की आंशिक भिन्नों का उपयोग कर सकते हैं। इन रूपों का उपयोग करके हम आसानी से उन भिन्नों को समाकलित कर सकते हैं जो निम्न तालिका में दिए गए समान रूपों में हैं। | |||
आंशिक भिन्नों द्वारा समाकलन की विधि | |||
आंशिक भिन्नों द्वारा समाकलन की विधि एक सरल प्रक्रिया है। आइए आंशिक भिन्नों द्वारा समाकलन की विधि को एक उदाहरण से समझें। हमारे पास है: | |||
∫[6/(x<sup>2</sup>-1)]dx | |||
Since we know: x<sup>2</sup>-1 = (x+1)(x-1) | |||
Hence we can write: | |||
∫[6/(x<sup>2</sup>-1)]dx = ∫[6/(x+1)(x-1)]dx | |||
अब इस प्रकार के परिमेय रूप के लिए आंशिक भिन्न के रूप का उपयोग करने पर, हमें प्राप्त होता है: | |||
6/(x+1)(x-1) = A/(x-1) + B/(x+1) | |||
Now, we have to find the value of A and B, making a common denominator on both sides. | |||
6/(x+1)(x-1) = [A/(x-1)][(x+1)/(x+1)] + [B/(x+1)][(x-1)/(x-1)] | |||
6/(x+1)(x-1)= [A(x+1) + B (x-1)]/(x-1)(x+1) | |||
Further we have the denominators on both the sides as equal, and hence the numerators will also be equal. | |||
6 = [A(x+1) + B (x-1)] | |||
On solving we get, | |||
A = 3, and B = -3 | |||
Hence, we can write | |||
6/(x+1)(x-1) = 3/(x-1) + (-3)/(x+1) | |||
Now, we can write: | |||
∫[6/(x<sup>2</sup>-1)]dx = ∫[3/(x-1) - 3/(x+1)]dx | |||
On solving, we will get: | |||
∫[6/(x<sup>2</sup>-1)]dx = −3ln(|x+1|)+3ln(|x−1|)+C | |||
[[File:आंशिक भिन्नों द्वारा समाकलन.jpg|thumb|356x356px|आंशिक भिन्नों द्वारा समाकलन]] | |||
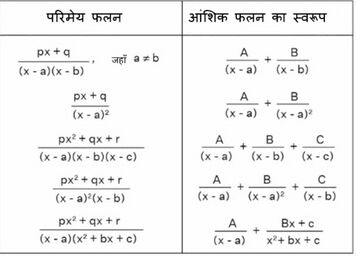
Suppose we have to find y=∫P(x)Q(x)dx where P(x)Q(x) is an improper rational function. We reduce it in such a way that P(x)Q(x)=T(x)+P1(x)Q(x). Here, T(x) is polynomial in x and P1(x)Q(x) is proper rational function. The following table shows some rational functions and their corresponding form of partial fractions. | |||
For example, let's find the integral of f(x)=1(x+1)(x+2) using integration by partial fractions.By using partial fraction we have | |||
1(x+1)(x+2)=Ax+1+Bx+2⋯(1). | |||
We will determine the values of A and B. | |||
On comparing in equation (1), we get 1=A(x+2)+B(x+1).From this, we have a set of two linear equations. | |||
A+B=0 and 2A+B =1 | |||
On solving these equations we get, A=1 and B=-1. | |||
So, equation (1) can be written as 1(x+1)(x+2)=1x+1−1x+2. | |||
Now, solving the integral | |||
∫(1(x+1)(x+2))dx=∫(1x+1−1x+2)dx=log|x+1|−log|x+2|+C=log∣∣∣x+1x+2∣∣∣+C | |||
[[Category:समाकलन]][[Category:गणित]][[Category:कक्षा-12]] | [[Category:समाकलन]][[Category:गणित]][[Category:कक्षा-12]] | ||
Revision as of 21:17, 3 December 2024
आंशिक भिन्नों द्वारा समाकलन एक ऐसी विधि है जिसका उपयोग किसी परिमेय भिन्न समाकलन को विघटित करने और फिर समाकलित करने के लिए किया जाता है जिसके हर में जटिल पद होते हैं। आंशिक भिन्न का उपयोग करके, हम व्यंजक की गणना करते हैं और उसे सरल पदों में विघटित करते हैं ताकि हम इस प्रकार प्राप्त व्यंजक की आसानी से गणना या एकीकरण कर सकें।
आंशिक भिन्नों द्वारा समाकलन में मूल विचार हर को गुणनखंडित करना और फिर उन्हें दो अलग-अलग भिन्नों में विघटित करना है जहाँ हर क्रमशः गुणनखंड होते हैं और अंश की गणना उपयुक्त रूप से की जाती है। आइए आंशिक भिन्नों द्वारा समाकलन में उपयोग किए जाने वाले विभिन्न रूपों और विभिन्न विधियों के बारे में अधिक जानें।
आंशिक भिन्नों द्वारा एकीकरण क्या है?
आंशिक भिन्नों द्वारा एकीकरण एकीकरण की तीन विधियों में से एक है। इस विधि में, हम उचित परिमेय भिन्न को सरल परिमेय भिन्नों के योग में विघटित करते हैं। परिमेय भिन्न को सरल परिमेय भिन्नों में विघटित करना हमेशा संभव होता है और यह आंशिक भिन्न अपघटन नामक प्रक्रिया द्वारा किया जाता है। आइए इसे एक उदाहरण की मदद से समझते हैं। मान लीजिए हमारे पास 5/6 है, तो हम इसे 5/6 = 1/2 + 1/3 के रूप में विघटित कर सकते हैं, इसी तरह, हम दो आंशिक भिन्नों को बीजगणितीय रूप से विघटित करके ऐसा करते हैं। मान लीजिए हमारे पास है:
2/(x+1) - 1/x
on adding we will get
2/(x+1) - 1/x = (x-1)/(x2+x).
Now if we have
(x-1)/(x2+x)
so we can decompose it into
(x-1)/(x2+x) = 2/(x+1) - 1/x
इस प्रकार आंशिक भिन्नों को सरल पदों में विघटित कर दिया गया है। इसलिए अब परिणामी पदों को एकीकृत करना अपेक्षाकृत आसान कार्य होगा। आंशिक भिन्नों द्वारा एकीकरण इस प्रकार होगा:
∫[f(x)/g(x)]dx = ∫[p(x)/q(x)]dx + ∫[r(x)/s(x)]dx
where
- f(x)/g(x) = p(x)/q(x) + r(x)/s(x) and
- g(x) = q(x).s(x)
आंशिक भिन्नों द्वारा समाकलन में प्रयुक्त रूप
आंशिक भिन्नों द्वारा समाकलन में, हम उचित परिमेय भिन्नों के विशिष्ट रूपों को विघटित करने के लिए कुछ विशेष प्रकार की आंशिक भिन्नों का उपयोग कर सकते हैं। इन रूपों का उपयोग करके हम आसानी से उन भिन्नों को समाकलित कर सकते हैं जो निम्न तालिका में दिए गए समान रूपों में हैं।
आंशिक भिन्नों द्वारा समाकलन की विधि
आंशिक भिन्नों द्वारा समाकलन की विधि एक सरल प्रक्रिया है। आइए आंशिक भिन्नों द्वारा समाकलन की विधि को एक उदाहरण से समझें। हमारे पास है:
∫[6/(x2-1)]dx
Since we know: x2-1 = (x+1)(x-1)
Hence we can write:
∫[6/(x2-1)]dx = ∫[6/(x+1)(x-1)]dx
अब इस प्रकार के परिमेय रूप के लिए आंशिक भिन्न के रूप का उपयोग करने पर, हमें प्राप्त होता है:
6/(x+1)(x-1) = A/(x-1) + B/(x+1)
Now, we have to find the value of A and B, making a common denominator on both sides.
6/(x+1)(x-1) = [A/(x-1)][(x+1)/(x+1)] + [B/(x+1)][(x-1)/(x-1)]
6/(x+1)(x-1)= [A(x+1) + B (x-1)]/(x-1)(x+1)
Further we have the denominators on both the sides as equal, and hence the numerators will also be equal.
6 = [A(x+1) + B (x-1)]
On solving we get,
A = 3, and B = -3
Hence, we can write
6/(x+1)(x-1) = 3/(x-1) + (-3)/(x+1)
Now, we can write:
∫[6/(x2-1)]dx = ∫[3/(x-1) - 3/(x+1)]dx
On solving, we will get:
∫[6/(x2-1)]dx = −3ln(|x+1|)+3ln(|x−1|)+C
Suppose we have to find y=∫P(x)Q(x)dx where P(x)Q(x) is an improper rational function. We reduce it in such a way that P(x)Q(x)=T(x)+P1(x)Q(x). Here, T(x) is polynomial in x and P1(x)Q(x) is proper rational function. The following table shows some rational functions and their corresponding form of partial fractions.
For example, let's find the integral of f(x)=1(x+1)(x+2) using integration by partial fractions.By using partial fraction we have
1(x+1)(x+2)=Ax+1+Bx+2⋯(1).
We will determine the values of A and B.
On comparing in equation (1), we get 1=A(x+2)+B(x+1).From this, we have a set of two linear equations.
A+B=0 and 2A+B =1
On solving these equations we get, A=1 and B=-1.
So, equation (1) can be written as 1(x+1)(x+2)=1x+1−1x+2.
Now, solving the integral
∫(1(x+1)(x+2))dx=∫(1x+1−1x+2)dx=log|x+1|−log|x+2|+C=log∣∣∣x+1x+2∣∣∣+C