केंद्र से जीवा पर लंब: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
In Mathematics, a chord is a line segment that joins two points on the circumference of a circle. We know that the longest chord of a circle is a diameter that passes through the centre of a circle. In this article, the theorem related to the perpendicular from the centre to a circle and its proof, and the converse of this theorem in detail. | |||
== Perpendicular from the Centre to a Chord – Theorem and Proof == | |||
=== Theorem: === | |||
The perpendicular from the centre of a circle to a chord bisects the chord. | |||
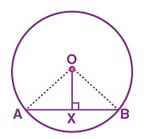
'''Proof:'''[[File:Circle-1.jpg|alt=Fig. 1|thumb|150x150px|Fig. 1]] | |||
Consider a circle with centre <math>O</math> shown in Fig. 1 | |||
<math>AB</math> is a chord such that the line <math>OX</math> is perpendicular to the chord <math>AB</math>. (<math>OX\perp AB</math>) | |||
We need to prove: <math>AX=BX</math> | |||
Consider two triangles <math>OAX</math> and <math>OBX</math> | |||
<math>\angle OXA =\angle OXB=90^\circ </math> | |||
<math>OX=OX</math> (Common side) | |||
<math>OA=OB</math> (Radii) | |||
By using the RHS rule, we can prove that the triangle <math>OAX</math> is congruent to <math>OBX</math>. | |||
Therefore, | |||
<math>\triangle OAX \cong \triangle OBX </math> | |||
Hence, we can say that <math>AX=BX</math> ( Using CPCT) | |||
Thus, the perpendicular from the centre of a circle to a chord bisects the chord, is proved. | |||
=== The Converse of this Theorem: === | |||
The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord | |||
'''Proof:''' | |||
Consider the Fig. 1 | |||
Assume that <math>AB</math> is the chord of a circle with centre <math>O</math>. | |||
The centre <math>O</math> is joined to the midpoint <math>X</math> of the chord <math>AB</math>. | |||
Now, we need to prove <math>OX\perp AB</math> | |||
Join <math>OA</math> and <math>OB</math> and the two triangles formed are <math>OAX</math> and <math>OBX</math>. | |||
Here, | |||
<math>OA=OB</math> (Radii) | |||
<math>OX=OX</math> (Common side) | |||
<math>AX=BX</math> (As, <math>X</math> is the midpoint of AB) | |||
Therefore, we can say that <math>\triangle OAX \cong \triangle OBX </math>. | |||
Thus, by using the RHS rule, we get | |||
<math>\angle OXA =\angle OXB=90^\circ </math> | |||
This proves that the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.Hence, the converse of this theorem is proved. | |||
[[Category:वृत्त]][[Category:कक्षा-9]][[Category:गणित]] | [[Category:वृत्त]][[Category:कक्षा-9]][[Category:गणित]] | ||
Revision as of 11:16, 18 September 2024
In Mathematics, a chord is a line segment that joins two points on the circumference of a circle. We know that the longest chord of a circle is a diameter that passes through the centre of a circle. In this article, the theorem related to the perpendicular from the centre to a circle and its proof, and the converse of this theorem in detail.
Perpendicular from the Centre to a Chord – Theorem and Proof
Theorem:
The perpendicular from the centre of a circle to a chord bisects the chord.
Proof:
Consider a circle with centre shown in Fig. 1
is a chord such that the line is perpendicular to the chord . ()
We need to prove:
Consider two triangles and
(Common side)
(Radii)
By using the RHS rule, we can prove that the triangle is congruent to .
Therefore,
Hence, we can say that ( Using CPCT)
Thus, the perpendicular from the centre of a circle to a chord bisects the chord, is proved.
The Converse of this Theorem:
The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord
Proof:
Consider the Fig. 1
Assume that is the chord of a circle with centre .
The centre is joined to the midpoint of the chord .
Now, we need to prove
Join and and the two triangles formed are and .
Here,
(Radii)
(Common side)
(As, is the midpoint of AB)
Therefore, we can say that .
Thus, by using the RHS rule, we get
This proves that the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.Hence, the converse of this theorem is proved.