विभाजन-सूत्र: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
The Section formula is used to find the coordinates of the point that divides a line segment (externally or internally) into some ratio. | |||
== Derivation of Section Formula == | |||
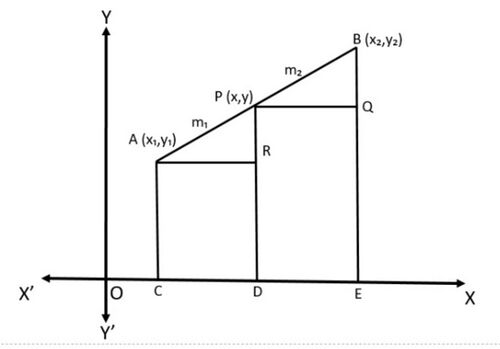
[[File:Section Formula.jpg|alt=Fig 1 - Section Formula|none|thumb|500x500px|Fig 1 - Section Formula]] | |||
Consider any two points <math>A(x_1,y_1)</math> and <math>B(x_2,y_2)</math> and assume that <math>P(x,y)</math> divides <math>AB</math> internally in the ratio <math>m_1:m_2</math> , | |||
i.e., <math>\frac{PA}{PB}=\frac{m_1}{m_2}</math> (see Fig. 1). | |||
Draw <math>AC,PD,BE</math> perpendicular to the <math>x-</math>axis. Draw <math>AR,PQ</math> parallel to the <math>x-</math>axis. Then, by the <math>AA</math> similarity criterion, | |||
<math>\bigtriangleup PAR\sim \bigtriangleup BPQ</math> | |||
<math>\frac{PA}{PB}=\frac{AR}{PQ}=\frac{PR}{BQ} ....... (1)</math> | |||
<math>AR=CD=OD-OC=x-x_1</math> | |||
<math>PQ=DE=OE-OD=x_2-x</math> | |||
<math>PR=PD-RD=PD-AC=y-y_1</math> | |||
<math>BQ=BE-QE=BE-PD=y_2-y</math> | |||
Substituting in <math> (1)</math> we get | |||
<math>\frac{m_1}{m_2}=\frac{x-x_1}{x_2-x}=\frac{y-y_1}{y_2-y}</math> | |||
Taking <math>\frac{m_1}{m_2}=\frac{x-x_1}{x_2-x}</math> | |||
<math>m_1x_2-m_1x=m_2x-m_2x_1</math> | |||
<math>m_1x_2+m_2x_1=m_2x+m_1x</math> | |||
<math>m_1x_2+m_2x_1=x(m_2+m_1)</math> | |||
<math>x=\frac{m_1x_2+m_2x_1}{m_1+m_2}</math> | |||
Taking <math>\frac{m_1}{m_2}=\frac{y-y_1}{y_2-y}</math> | |||
<math>m_1y_2-m_1y=m_2y-m_2y_1</math> | |||
<math>m_1y_2+m_2y_1=m_2y+m_1y</math> | |||
<math>m_1y_2+m_2y_1=y(m_2+m_1) </math> | |||
<math>y=\frac{m_1y_2+m_2y_1}{m_1+m_2}</math> | |||
So, the coordinates of the point <math>P(x,y)</math> which divides the line segment joining the points <math>A(x_1,y_1)</math> and <math>B(x_2,y_2)</math>, internally, in the ratio <math>m_1:m_2</math> are <math>\left (\frac{m_1x_2+m_2x_1}{m_1+m_2},\frac{m_1y_2+m_2y_1}{m_1+m_2} \right )</math> is the section formula. | |||
=== Example === | |||
Find the coordinates of the point which divides the line segment joining the points <math>(4,-3)</math> and <math>(8,5)</math> in the ratio <math>3:1</math> internally. | |||
'''Solution''' : Let <math>P(x,y)</math> be the required point. | |||
<math>x_1=4,y_1=-3</math> | |||
<math>x_2=8,y_2=5</math> | |||
<math>m_1=3,m_2=1</math> | |||
Using the section formula, we get | |||
<math>x=\frac{m_1x_2+m_2x_1}{m_1+m_2}</math> | |||
<math>x=\frac{3 \times 8+ 1 \times 4}{3+1}=7 </math> | |||
<math>y=\frac{m_1y_2+m_2y_1}{m_1+m_2}</math> | |||
<math>y=\frac{3 \times 5+ 1 \times -3}{3+1}=3 </math> | |||
Therefore <math>(7,3)</math> is the required point. | |||
[[Category:निर्देशांक ज्यामिति]][[Category:गणित]][[Category:कक्षा-10]] | [[Category:निर्देशांक ज्यामिति]][[Category:गणित]][[Category:कक्षा-10]] | ||
Revision as of 09:57, 19 June 2024
The Section formula is used to find the coordinates of the point that divides a line segment (externally or internally) into some ratio.
Derivation of Section Formula
Consider any two points and and assume that divides internally in the ratio ,
i.e., (see Fig. 1).
Draw perpendicular to the axis. Draw parallel to the axis. Then, by the similarity criterion,
Substituting in we get
Taking
Taking
So, the coordinates of the point which divides the line segment joining the points and , internally, in the ratio are is the section formula.
Example
Find the coordinates of the point which divides the line segment joining the points and in the ratio internally.
Solution : Let be the required point.
Using the section formula, we get
Therefore is the required point.