ऊँचाइयाँ और दूरियाँ: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
The topic heights and distance is one of the applications of Trigonometry, which is extensively used in real-life. The words height and distance are frequently used in the trigonometry while dealing with its applications. In the height and distances application of trigonometry, the following concepts are included: | |||
* Measuring the heights of towers | |||
* Determining the distance of the shore from the sea | |||
* Finding the distance between two celestial bodies | |||
[[File:Heights and Distances.jpg|alt=Fig. 1 - Heights and distances|thumb|500x500px|Fig. 1 - Heights and distances]] | |||
== Line of Sight == | |||
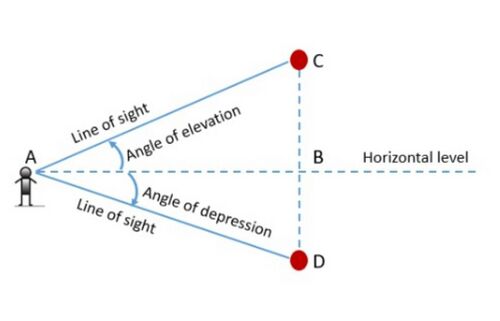
The line which is drawn from the eyes of the observer to the point being viewed on the object is known as the line of sight. | |||
== Angle of Elevation == | |||
The angle of elevation of the point on the object (above horizontal level) viewed by the observer is the angle which is formed by the line of sight with the horizontal level. | |||
== Angle of Depression == | |||
The angle of depression of the point on the object (below horizontal level) viewed by the observer is the angle which is formed by the line of sight with the horizontal level. | |||
== How to find heights and distances == | |||
The height or length of an object or the distance between two distant objects can be determined with the help of trigonometric ratios. | |||
For example, in fig.1, a person is looking at the top of the object. <math>AB</math> is horizontal level. This level is the line parallel to ground passing through the observer’s eyes. <math>AC</math> is known as the line of sight. <math>\angle CAB</math> is called the angle of elevation. Similarly, in fig. 1, person is looking down at a object. <math>AB</math> is horizontal level. This level is the line parallel to ground passing through the observer’s eyes. <math>AD</math> is known as the line of sight. <math>\angle BAD</math> is called the angle of depression. | |||
[[File:Heights and Distances - problem 1.jpg|alt=Fig. 2 - Problem|thumb|500x500px|Fig. 2 - Problem]] | |||
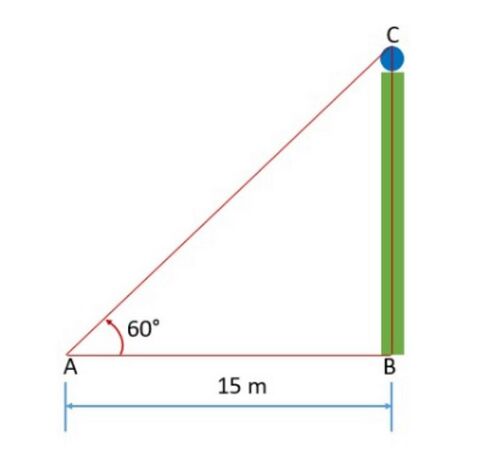
'''Example''': A tower stands vertically on the ground. From a point on the ground, which is <math>15 </math>m away from the foot of the tower, the angle of elevation of the top of the tower is found to be <math>60^\circ</math>. Find the height of the tower. | |||
'''Solution:''' To solve the problem, we choose the trigonometric ratio <math>tan \ 60^\circ</math> (or <math>cot \ 60^\circ</math>), as the ratio involves <math>AB</math> and <math>BC</math> . | |||
<math>tan \ 60^\circ =\frac{BC}{AB}</math> | |||
<math>\sqrt{3} =\frac{BC}{15}</math> | |||
<math>BC=15\sqrt{3}</math> | |||
Hence, the height of the tower is <math>15\sqrt{3}</math> m. | |||
[[Category:त्रिकोणमिति के कुछ अनुप्रयोग]][[Category:गणित]][[Category:कक्षा-10]] | [[Category:त्रिकोणमिति के कुछ अनुप्रयोग]][[Category:गणित]][[Category:कक्षा-10]] | ||
Revision as of 14:38, 14 June 2024
The topic heights and distance is one of the applications of Trigonometry, which is extensively used in real-life. The words height and distance are frequently used in the trigonometry while dealing with its applications. In the height and distances application of trigonometry, the following concepts are included:
- Measuring the heights of towers
- Determining the distance of the shore from the sea
- Finding the distance between two celestial bodies
Line of Sight
The line which is drawn from the eyes of the observer to the point being viewed on the object is known as the line of sight.
Angle of Elevation
The angle of elevation of the point on the object (above horizontal level) viewed by the observer is the angle which is formed by the line of sight with the horizontal level.
Angle of Depression
The angle of depression of the point on the object (below horizontal level) viewed by the observer is the angle which is formed by the line of sight with the horizontal level.
How to find heights and distances
The height or length of an object or the distance between two distant objects can be determined with the help of trigonometric ratios.
For example, in fig.1, a person is looking at the top of the object. is horizontal level. This level is the line parallel to ground passing through the observer’s eyes. is known as the line of sight. is called the angle of elevation. Similarly, in fig. 1, person is looking down at a object. is horizontal level. This level is the line parallel to ground passing through the observer’s eyes. is known as the line of sight. is called the angle of depression.
Example: A tower stands vertically on the ground. From a point on the ground, which is m away from the foot of the tower, the angle of elevation of the top of the tower is found to be . Find the height of the tower.
Solution: To solve the problem, we choose the trigonometric ratio (or ), as the ratio involves and .
Hence, the height of the tower is m.