वृद्धि मॉडल: Difference between revisions
Listen
Jaya agarwal (talk | contribs) |
mNo edit summary |
||
| Line 18: | Line 18: | ||
<math>\frac{dN}{dt} = (b-d) \times N</math> | <math>\frac{dN}{dt} = (b-d) \times N</math> | ||
अगर,<math>(b-d) = r</math> | |||
तब, <math>\frac{dN}{dt} = rN</math> | तब, <math>\frac{dN}{dt} = rN</math> | ||
Revision as of 14:14, 16 October 2023
क्या समय के साथ जनसंख्या कोई वृद्धि दर्शाती है? प्रकृति में, हम शायद ही कभी किसी प्रजाति को अलग और एकल पाते हैं I सभी भौगोलिक क्षेत्र में समूहों में रहते हैं, समान संसाधनों के लिए या प्रतिस्पर्धा करते हैं या उन्हें साझा करते हैं I किसी भी प्रजाति के लिए जनसंख्या का आकार एक स्थिर कारक नहीं है। यह भोजन की उपलब्धता, शिकार का दबाव, प्रतिकूल मौसम और समय में परिवर्तन सहित विभिन्न कारकों के आधार पर बदलती रहती है।
एक जनसंख्या में कुछ ऐसे गुण होते हैं जो एक व्यक्तिगत जीव में नहीं होते हैं। उनमें से एक गुण है वृद्धि मॉडल जो सिर्फ जनसंख्या में पाया जाता हैI यह वृद्धि मॉडल जनसंख्या में बुनियादी विकास प्रवृत्ति का वर्णन करते हैं। आइए उन्हें समझें-
परिभाषा
वृद्धि मॉडल समय के साथ जनसंख्या की वृद्धि के विशिष्ट और पूर्वानुमानित पैटर्न को दर्शाता है। जनसंख्या की वृद्धि, भोजन की उपलब्धता, प्राकृतिक वास की स्थिति तथा अन्य जैविक एवं अजैविक कारकों की उपस्थिति के अनुसार होती है।
प्रकार
मॉडल दो मुख्य प्रकार के होते हैं:
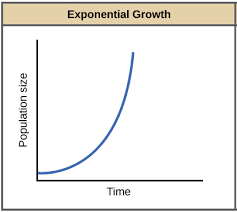
चरघातांकी वृद्धि:
एक आदर्श स्थिति में जहां भोजन और संसाधनों की असीमित आपूर्ति होती है, जनसंख्या वृद्धि एक चरघातांकी वृद्धि क्रम करती है। आदर्श रूप से, जब प्रत्येक प्रजाति के आवास में संसाधन असीमित हों तो प्रजाति अपनी संख्या में वृद्धि करने की अपनी जन्मजात क्षमता को पूरी तरह से साकार करने की क्षमता रखती है।
आकार की जनसंख्या में, अगर जन्म दर को के रूप में दर्शाया जाए और मृत्यु दर को के रूप में दर्शाया जाए, तब N के परिवर्तन की दर (वृद्धि होना या कम होना) इकाई समयावधि, के दौरान कुछ इस प्रकार दी जा सकती है-
अगर,
तब,
इस समीकरण में को 'प्राकृतिक वृद्धि की आंतरिक दर' कहा जाता है और जनसंख्या वृद्धि पर कोई जैविक या अजैविक कारक के प्रभावों का आकलन करने के लिए चुना गया है।
उपरोक्त समीकरण चरघातांकी या ज्यामितीय वृद्धि का वर्णन करता है I जब हम समय के संबंध में आलेखित करते हैं तो परिणाम में जे-आकार का वक्र बनता है। यदि आप बेसिक कैलकुलस से परिचित हैं, आप चरघातांकी वृद्धि समीकरण का अभिन्न रूप (integral form) प्राप्त कर सकते हैं I आइये देखे कैसे-
जहां, समय के बाद जनसंख्या घनत्व
समय शून्य पर जनसंख्या घनत्व
प्राकृतिक वृद्धि की आंतरिक दर
प्राकृतिक लघुगणक का आधार
उदाहरण:
चरघातांकी वृद्धि मॉडल के वास्तविक उदाहरणों में बैक्टीरिया की चरघातांकी वृद्धि और बारिश के मौसम में पतंगों की चरघातांकी वृद्धि प्रतिनिधित्व करती है I
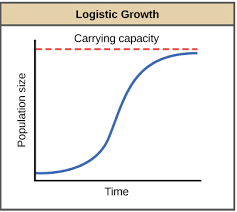
संभार तंत्र वृद्धि:
संभार तंत्र वृद्धि मॉडल 'योग्यतम की उत्तरजीविता' की अवधारणा को परिभाषित करता है। इस प्रकार, यह इस तथ्य पर विचार करता है कि प्रकृति में संसाधन समाप्त हो सकते हैं। 'वहन क्षमता' शब्द संसाधनों की उस सीमा को परिभाषित करता है जिसके आगे वे किसी भी संख्या में जीवों का समर्थन नहीं कर सकते हैं। इस वहन क्षमता को K के रूप में दर्शाया गया है। इसे के बारे में और ज्ञानार्जन करते है-
सीमित संसाधनों के लिए व्यक्तियों/प्रजातियों के बीच प्रतिस्पर्धा होती है। अंततः, 'सबसे योग्य' ही जीवित रहता है और प्रजनन करता है। प्रकृति में, किसी दिए गए क्षेत्र के पास अधिकतम संभव संख्या के समर्थन के लिए पर्याप्त संसाधन होते हैं, जिसके आगे कोई वृद्धि संभव नहीं होती। हम इस सीमा को प्रकृति की वहन क्षमता (K) कहते हैं उस क्षेत्र में रह रही प्रजाति के लिए I
सीमित संसाधनों की उपलब्धता से तीव्र वृद्धि नहीं दिखाई जा सकती। परिणामस्वरूप, संभार तंत्र वृद्धि ग्राफ़ में एक अंतराल चरण होगा, उसके बाद एक घातीय चरण, फिर एक गिरावट चरण और अंततः एक अनंतस्पर्शी चरण होगा। इसे वर्हुल्स्ट-पर्ल लॉजिस्टिक ग्रोथ के रूप में जाना जाता है और इसे समीकरण का उपयोग करके कुछ इस प्रकार दर्शाया जाता है:
जहां, समय में जनसंख्या घनत्व
प्राकृतिक वृद्धि की आंतरिक दर
प्रकृति की वहन क्षमता
समय के संबंध में के प्लॉट के परिणामस्वरूप सिग्मॉइड वक्र बनता है।
अधिकांश प्रजातियों के लिए विकास के संसाधन सीमित हैं, इसके कारण संभार तंत्र वृद्धि मॉडल अधिक यथार्थवादी माना जाता है।
उदाहरण:
मानव जनसंख्या एक संभार तंत्र वृद्धि का प्रतिनिधित्व करती है।