समुच्चयों पर संक्रियाएँ: Difference between revisions
(image added) |
(content added) |
||
| Line 22: | Line 22: | ||
=== परिभाषा === | === परिभाषा === | ||
दो समुच्चय <math>A</math> और <math>B</math> का सम्मिलन समुच्चय <math>C</math> है जिसमें वे सभी | दो समुच्चय <math>A</math> और <math>B</math> का सम्मिलन समुच्चय <math>C</math> है जिसमें वे सभी अवयव समिलित होते हैं जो या तो <math>A</math> में हैं या <math>B</math> में हैं जिनमें वे भी समिलित हैं जो दोनों में हैं)। प्रतीकों में हम https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=7534bf4c2952d5376a5e54699a60955f&mode=mathml लिखते हैं। दो समुच्चयों के सम्मिलन को वेन आरेख द्वारा दर्शाया जा सकता है, जैसा चित्र-1 में दर्शाया गया है। | ||
चित्र-1 में छायांकित भाग <math>A \cup B</math> को दर्शाता है। | चित्र-1 में छायांकित भाग <math>A \cup B</math> को दर्शाता है। | ||
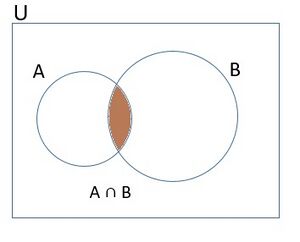
[[File:Intersection - Sets.jpg|thumb|चित्र-2 समुच्चयों का सर्वनिष्ट]] | |||
== समुच्चयों का सर्वनिष्ट == | |||
यदि दो समुच्चय <math>A</math> और <math>B</math> दिए गए हैं, तो <math>A</math> और <math>B</math> का सर्वनिष्ट उन सभी तत्वों का समुच्चय है जो <math>A</math> और <math>B</math> दोनों के लिए उभयनिष्ठ हैं। सर्वनिष्ट को प्रतीक ∩ द्वारा दर्शाया जाता है। प्रतीकात्मक रूप से, हम https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=08f9fad30ed594e7591a3e04a8d7774c&mode=mathml लिखते हैं, जहां <math>x</math> दोनों समुच्चयों <math>A</math> और <math>B</math> का उभयनिष्ठ अवयव है। दो समुच्चयों के सर्वनिष्ट को वेन आरेख द्वारा दर्शाया जा सकता है। | |||
जैसा चित्र-2 में दर्शाया गया है। | |||
'''उदाहरण''' | |||
मान लीजिए https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=a4f3595fe5a52eb573de1997bfe8e993&mode=mathml और https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=d4258e214ba37604d1ed55319268c582&mode=mathml | |||
यहाँ https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=88e83b543fda0b5159e0579cb994d4b2&mode=mathml साथ ही https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=95d8981b7d6497ec10f44dc8fbc98368&mode=mathml और https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=2939c58616be9e3b6cf82671ae58c8d6&mode=mathml | |||
== समुच्चयों का अंतर == | == समुच्चयों का अंतर == | ||
[[Category:समुच्चय]][[Category:कक्षा-11]][[Category:गणित]] | [[Category:समुच्चय]][[Category:कक्षा-11]][[Category:गणित]] | ||
Revision as of 17:20, 29 November 2023
जब हम संख्याओं के युग्म पर जोड़ और गुणा की क्रिया करते हैं तो हमें एक और संख्या प्राप्त होती है। इसी प्रकार, जब हम दो समुच्चयों पर संचालन करते हैं, तो हमें एक और समुच्चय मिलता है। अब हम समुच्चय पर कुछ निश्चित संचालनों को परिभाषित करेंगे और उनके गुणों को समझेंगे।
अब से, हम अपने सभी समुच्चयों को किसी सार्वत्रिक समुच्चय के उपसमुच्चय के रूप में संदर्भित करेंगे।
समुच्चयों का सम्मिलन
मान लीजिए कि और कोई दो समुच्चय हैं। समुच्चय के सम्मिलन का अर्थ है उभयनिष्ठ अवयवों को केवल एक बार रखते हुए और के सभी अवयवों को लेना। सम्मिलन को सूचित करने वाला प्रतीक है। प्रतीकात्मक रूप से, हम लिखते हैं,और इसे " यूनियन " के रूप में पढ़ा जाता है।
उदाहरण 1
मान लीजिए और
। यहां इन दोनों समुच्चयों के उभयनिष्ठ अवयव हैं, जिन्हें दिखाते समय मात्र एक बार लिया जाता है।
उदाहरण 2
मान लीजिए और
यहाँ , का एक उपसमुच्चय है। समुच्चय और उसके उपसमुच्चय का सम्मिलन समुच्चय ही है।
अर्थात यदि तब
परिभाषा
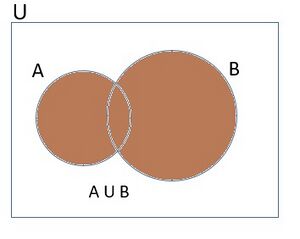
दो समुच्चय और का सम्मिलन समुच्चय है जिसमें वे सभी अवयव समिलित होते हैं जो या तो में हैं या में हैं जिनमें वे भी समिलित हैं जो दोनों में हैं)। प्रतीकों में हम https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=7534bf4c2952d5376a5e54699a60955f&mode=mathml लिखते हैं। दो समुच्चयों के सम्मिलन को वेन आरेख द्वारा दर्शाया जा सकता है, जैसा चित्र-1 में दर्शाया गया है।
चित्र-1 में छायांकित भाग को दर्शाता है।
समुच्चयों का सर्वनिष्ट
यदि दो समुच्चय और दिए गए हैं, तो और का सर्वनिष्ट उन सभी तत्वों का समुच्चय है जो और दोनों के लिए उभयनिष्ठ हैं। सर्वनिष्ट को प्रतीक ∩ द्वारा दर्शाया जाता है। प्रतीकात्मक रूप से, हम https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=08f9fad30ed594e7591a3e04a8d7774c&mode=mathml लिखते हैं, जहां दोनों समुच्चयों और का उभयनिष्ठ अवयव है। दो समुच्चयों के सर्वनिष्ट को वेन आरेख द्वारा दर्शाया जा सकता है।
जैसा चित्र-2 में दर्शाया गया है।
उदाहरण
मान लीजिए https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=a4f3595fe5a52eb573de1997bfe8e993&mode=mathml और https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=d4258e214ba37604d1ed55319268c582&mode=mathml
यहाँ https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=88e83b543fda0b5159e0579cb994d4b2&mode=mathml साथ ही https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=95d8981b7d6497ec10f44dc8fbc98368&mode=mathml और https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=2939c58616be9e3b6cf82671ae58c8d6&mode=mathml