यूक्लिड: Difference between revisions
Jaya agarwal (talk | contribs) |
|||
| Line 20: | Line 20: | ||
=== यूक्लिड के अभिधारणाएँ === | === यूक्लिड के अभिधारणाएँ === | ||
[[Category:यूक्लिड की ज्यामिति]][[Category:कक्षा-9]][[Category:गणित]] | |||
ज्यामिति में, अभिधारणा एक कथन है जिसे बुनियादी ज्यामितीय सिद्धांतों के आधार पर सत्य माना जाता है। अभिधारणा का एक उदाहरण यह कथन है "किसी भी दो बिंदुओं से होकर एक ही रेखा खींची जा सकती है।" | |||
'''अभिधारणा 1''': किसी एक बिंदु से किसी दूसरे बिंदु तक एक सीधी रेखा खींची जा सकती है। | |||
यह अभिधारणा हमें बताती है कि कम से कम एक सीधी रेखा दो अलग-अलग बिंदुओं से होकर गुजरती है, लेकिन यह नहीं कहती कि ऐसी एक से अधिक रेखाएँ नहीं हो सकतीं। हालाँकि, अपने काम में, यूक्लिड ने प्रायः यह मान लिया है, बिना बताए कि दो अलग-अलग बिंदुओं को जोड़ने वाली एक अनोखी रेखा होती है। हम इस परिणाम को एक अभिगृहीत के रूप में इस प्रकार बताते हैं: | |||
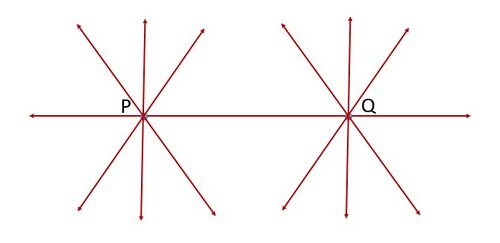
'''अभिगृहीत 5.1''': दो अलग-अलग बिंदु दिए गए हैं, एक अद्वितीय रेखा है जो उनसे होकर गुजरती है। कितनी रेखाएँ <math>P</math> से होकर गुजरती हैं और <math>Q</math> से भी होकर गुजरती हैं} (चित्र-1 देखें)? केवल एक, अर्थात् रेखा <math>PQ</math>। कितनी रेखाएँ <math>Q</math> से होकर गुजरती हैं और <math>P</math> से भी होकर गुजरती हैं? केवल एक, अर्थात् रेखा <math>PQ</math>। इस प्रकार, उपरोक्त कथन स्वतः स्पष्ट है, और इसलिए इसे एक अभिगृहीत के रूप में लिया जाता है | |||
[[File:Euclid-Axiom-5.1.jpg|left|thumb|चित्र-1 यूक्लिड-अभिगृहीत-5.1|500x500px]] | |||
'''अभिधारणा 2''': एक समाप्त रेखा अनिश्चित काल तक उत्पादित की जा सकती है। | |||
दूसरी अभिधारणा कहती है कि एक रेखाखंड को किसी भी ओर बढ़ाकर एक रेखा बनाई जा सकती है। चित्र-2 देखें | |||
[[File:Euclid-Postulate-2.jpg|left|thumb|चित्र-2 यूक्लिड-अभिधारणा-2|420x420px]] | |||
'''अभिधारणा 3''': किसी भी केंद्र और किसी भी त्रिज्या के साथ एक वृत्त खींचा जा सकता है। | |||
'''अभिधारणा 4''': सभी समकोण एक दूसरे के बराबर होते हैं। | |||
'''अभिधारणा 5''': यदि दो सीधी रेखाओं पर पड़ने वाली एक सीधी रेखा, एक ही तरफ के आंतरिक कोणों को मिलाकर दो समकोणों से कम बनाती है, तो दो सीधी रेखाएँ, यदि अनिश्चित रूप से बढ़ाई जाती हैं, तो उस तरफ मिलती हैं जिस तरफ कोणों का योग दो समकोणों से कम होता है। | |||
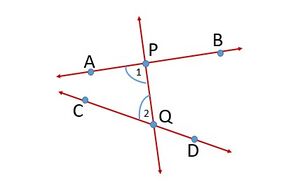
उदाहरण के लिए, चित्र-2 में रेखा <math>PQ</math> रेखाओं <math>AB</math> और <math>CD</math> पर इस प्रकार पड़ती है कि आंतरिक कोणों <math>1</math> और <math>2</math> का योग <math>PQ</math> के बाईं ओर <math>180^\circ </math> से कम है। इसलिए, रेखाएँ <math>AB</math> और <math>CD</math> अंततः <math>PQ</math> के बाईं ओर प्रतिच्छेद करेंगी। | |||
[[File:Euclid-Postulate-5.jpg|left|thumb|चित्र-3 यूक्लिड-अभिधारणा-5]] | |||
Revision as of 16:44, 16 October 2024
यूक्लिड को इतिहास में महान गणितज्ञों में से एक माना जाता है । उन्हें हम ज्यामिति के पिता के रूप में भी जानते हैं । उनके द्वारा प्रतिपादित ज्यामिति को हम यूक्लिडियन ज्यामिति कहते हैं । उन्हें मुख्य रूप से एलिमेंट्स ग्रंथ के लिए जाना जाता है, जिसने ज्यामिति की नींव स्थापित की , यूक्लिड के जीवन के बारे में बहुत कम जानकारी है, और अधिकांश जानकारी कई सदियों बाद अलेक्जेंड्रिया के दार्शनिक प्रोक्लस से मिलती है। आम तौर पर यह माना जाता है कि उन्होंने अपना करियर टॉलेमी प्रथम के अधीन अलेक्जेंड्रिया में बिताया और लगभग 300 ईसा पूर्व, प्लेटो के बाद और आर्किमिडीज़ से पहले जीवित रहे ।
यूक्लिड के अभिगृहीत और अभिधारणाएँ
लगभग 300 बी में यूक्लिड ने उसे समय तक ज्ञात गणित को क्षेत्र के संपूर्ण ज्ञान को एकत्रित किया तथा उसे एलिमेंट्स नामक अपनी प्रसिद्ध कृति के रूप में व्यवस्थित किया यूक्लिड ने कुछ गुणो को बिना सिद्ध किए सत्य मान लिया वह सत्य मान ली गई कल्पनाएँ वास्तव में सर्वव्यापी सत्य हैं , उन्हें दो वर्गों में बांटा गया है - अभिगृहीत और अभिधारणाएँ
आइए , हम अभिगृहीत और अभिधारणाओं के बारे में विस्तार पूर्वक जानते है ।
यूक्लिड के अभिगृहीत
- वे वस्तुएं जो एक ही वस्तु के बराबर हो परस्पर बराबर होती है ।
- यदि समान वस्तु को समान वस्तु में जोड़ा जाए तो पूर्ण भी बराबर होते हैं ।
- यदि समान वस्तु को समान से ही घटाया जाए तो शेषफल भी समान होते हैं।
- वह वस्तुएं जो परस्पर संपाती हो परस्पर बराबर भी होती हैं ।
- पूर्ण अपने भाग से बड़ा होता है।
- वह वस्तु जो एक ही वस्तु की दोगुनी हो परस्पर बराबर होती हैं ।
- वह वस्तुएं जो एक ही वस्तु की आधी हो परस्पर बराबर होती है।
यूक्लिड के अभिधारणाएँ
ज्यामिति में, अभिधारणा एक कथन है जिसे बुनियादी ज्यामितीय सिद्धांतों के आधार पर सत्य माना जाता है। अभिधारणा का एक उदाहरण यह कथन है "किसी भी दो बिंदुओं से होकर एक ही रेखा खींची जा सकती है।"
अभिधारणा 1: किसी एक बिंदु से किसी दूसरे बिंदु तक एक सीधी रेखा खींची जा सकती है।
यह अभिधारणा हमें बताती है कि कम से कम एक सीधी रेखा दो अलग-अलग बिंदुओं से होकर गुजरती है, लेकिन यह नहीं कहती कि ऐसी एक से अधिक रेखाएँ नहीं हो सकतीं। हालाँकि, अपने काम में, यूक्लिड ने प्रायः यह मान लिया है, बिना बताए कि दो अलग-अलग बिंदुओं को जोड़ने वाली एक अनोखी रेखा होती है। हम इस परिणाम को एक अभिगृहीत के रूप में इस प्रकार बताते हैं:
अभिगृहीत 5.1: दो अलग-अलग बिंदु दिए गए हैं, एक अद्वितीय रेखा है जो उनसे होकर गुजरती है। कितनी रेखाएँ से होकर गुजरती हैं और से भी होकर गुजरती हैं} (चित्र-1 देखें)? केवल एक, अर्थात् रेखा । कितनी रेखाएँ से होकर गुजरती हैं और से भी होकर गुजरती हैं? केवल एक, अर्थात् रेखा । इस प्रकार, उपरोक्त कथन स्वतः स्पष्ट है, और इसलिए इसे एक अभिगृहीत के रूप में लिया जाता है
अभिधारणा 2: एक समाप्त रेखा अनिश्चित काल तक उत्पादित की जा सकती है।
दूसरी अभिधारणा कहती है कि एक रेखाखंड को किसी भी ओर बढ़ाकर एक रेखा बनाई जा सकती है। चित्र-2 देखें
अभिधारणा 3: किसी भी केंद्र और किसी भी त्रिज्या के साथ एक वृत्त खींचा जा सकता है।
अभिधारणा 4: सभी समकोण एक दूसरे के बराबर होते हैं।
अभिधारणा 5: यदि दो सीधी रेखाओं पर पड़ने वाली एक सीधी रेखा, एक ही तरफ के आंतरिक कोणों को मिलाकर दो समकोणों से कम बनाती है, तो दो सीधी रेखाएँ, यदि अनिश्चित रूप से बढ़ाई जाती हैं, तो उस तरफ मिलती हैं जिस तरफ कोणों का योग दो समकोणों से कम होता है।
उदाहरण के लिए, चित्र-2 में रेखा रेखाओं और पर इस प्रकार पड़ती है कि आंतरिक कोणों और का योग के बाईं ओर से कम है। इसलिए, रेखाएँ और अंततः के बाईं ओर प्रतिच्छेद करेंगी।