|
|
| Line 5: |
Line 5: |
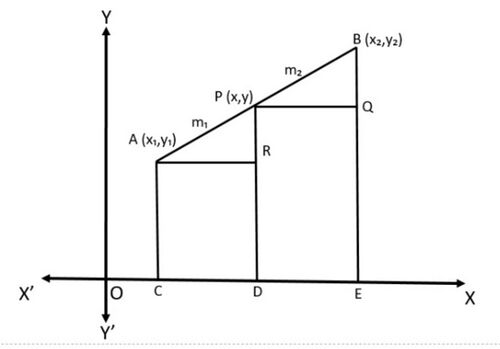
| किन्हीं दो बिंदुओं <math>A(x_1,y_1)</math> और <math>B(x_2,y_2)</math> पर विचार करें और मान लीजिये <math>P(x,y)</math>, <math>AB</math> को आंतरिक रूप से अनुपात <math>m_1:m_2</math> में विभाजित करता है। | | किन्हीं दो बिंदुओं <math>A(x_1,y_1)</math> और <math>B(x_2,y_2)</math> पर विचार करें और मान लीजिये <math>P(x,y)</math>, <math>AB</math> को आंतरिक रूप से अनुपात <math>m_1:m_2</math> में विभाजित करता है। |
|
| |
|
| i.e., <math>\frac{PA}{PB}=\frac{m_1}{m_2}</math> (चित्र 1 देखें)
| | अर्थात <math>\frac{PA}{PB}=\frac{m_1}{m_2}</math> (चित्र 1 देखें) |
| | |
| Draw <math>AC,PD,BE</math> perpendicular to the <math>x-</math>axis. Draw <math>AR,PQ</math> parallel to the <math>x-</math>axis. Then, by the <math>AA</math> similarity criterion,
| |
|
| |
|
| <math>x-</math>अक्ष पर लंबवत <math>AC,PD,BE</math> खींचें। <math>x-</math>अक्ष के समानांतर <math>AR,PQ</math> खींचें। फिर, <math>AA</math> समानता मानदंड से, | | <math>x-</math>अक्ष पर लंबवत <math>AC,PD,BE</math> खींचें। <math>x-</math>अक्ष के समानांतर <math>AR,PQ</math> खींचें। फिर, <math>AA</math> समानता मानदंड से, |
| Line 37: |
Line 35: |
|
| |
|
| <math>x=\frac{m_1x_2+m_2x_1}{m_1+m_2}</math> | | <math>x=\frac{m_1x_2+m_2x_1}{m_1+m_2}</math> |
| | |
|
| |
|
|
| |
|
विभाजन-सूत्र का उपयोग उस बिंदु के निर्देशांक ज्ञात करने के लिए किया जाता है जो किसी रेखाखंड को (बाह्य या आंतरिक रूप से) किसी अनुपात में विभाजित करता है।
विभाजन-सूत्र की व्युत्पत्ति
किन्हीं दो बिंदुओं  और
और  पर विचार करें और मान लीजिये
पर विचार करें और मान लीजिये  ,
,  को आंतरिक रूप से अनुपात
को आंतरिक रूप से अनुपात  में विभाजित करता है।
में विभाजित करता है।
अर्थात  (चित्र 1 देखें)
(चित्र 1 देखें)
 अक्ष पर लंबवत
अक्ष पर लंबवत  खींचें।
खींचें।  अक्ष के समानांतर
अक्ष के समानांतर  खींचें। फिर,
खींचें। फिर,  समानता मानदंड से,
समानता मानदंड से,






 प्रतिस्थापित करने पर हमें प्राप्त होता है
प्रतिस्थापित करने पर हमें प्राप्त होता है

 लेने पर
लेने पर




 लेने पर
लेने पर




इसलिए, बिंदु  के निर्देशांक जो बिंदु
के निर्देशांक जो बिंदु  और
और  को मिलाने वाले रेखाखंड को आंतरिक रूप से किस अनुपात में विभाजित करते हैं
को मिलाने वाले रेखाखंड को आंतरिक रूप से किस अनुपात में विभाजित करते हैं
 are
are  विभाजन-सूत्र है।
विभाजन-सूत्र है।
उदाहरण
उस बिंदु के निर्देशांक ज्ञात करें जो बिंदुओं  और
और  को मिलाने वाले रेखाखंड को
को मिलाने वाले रेखाखंड को  के अनुपात में आंतरिक रूप से विभाजित करता है।
के अनुपात में आंतरिक रूप से विभाजित करता है।
हल :  को वांछित बिंदु मान लें।
को वांछित बिंदु मान लें।



विभाजन-सूत्र का उपयोग करते हुए, हम प्राप्त करते




अतः  ही अभीष्ट बिंदु है।
ही अभीष्ट बिंदु है।