त्रिभुज का क्षेत्रफल - हीरोन के सूत्र द्वारा: Difference between revisions
(added content) |
(added content) |
||
| Line 11: | Line 11: | ||
The formula given by Heron about the area of a triangle, is also known as Hero’s formula. It is stated as: | The formula given by Heron about the area of a triangle, is also known as Hero’s formula. It is stated as: | ||
त्रिभुज का क्षेत्रफल =<math>\sqrt{s(s-a)(s-b)(s-c)}</math> | |||
जहाँ <math>a,b,c | |||
</math> | </math> त्रिभुज की भुजाएँ हैं, और <math>s</math>= अर्ध-परिधि, अर्थात, त्रिभुज की आधी परिधि | ||
<math>s=\frac{a+b+c}{2}</math> | <math>s=\frac{a+b+c}{2}</math> | ||
Revision as of 10:06, 8 September 2024
हीरोन का परिचय
हीरोन (10 ई.पू. - 75 ई.पू.) का जन्म संभवतः लगभग 10 ई.पू. में मिस्र के अलेक्जेंड्रिया में हुआ था। उन्होंने अनुप्रयुक्त गणित में कार्य किया। गणितीय और भौतिक विषयों पर उनके कार्य इतने अधिक और विविध हैं कि उन्हें इन क्षेत्रों में एक विश्वकोश लेखक माना जाता है। उनका ज्यामितीय कार्य मुख्यतः इससे संबंधित है
क्षेत्रमिति पर समस्याएं तीन पुस्तकों में लिखी गई हैं। पुस्तक-I में वर्गों, आयतों, त्रिभुजों, समलम्ब चतुर्भुजों (ट्रैपेज़िया), विभिन्न अन्य विशिष्ट चतुर्भुजों, नियमित बहुभुजों, वृत्तों, बेलनों की सतहों, शंकुओं, गोले आदि के क्षेत्रफल का वर्णन किया गया है। इस खंड में, त्रिभुज का क्षेत्रफल उसकी तीन भुजाओं के संदर्भ में हीरोन ने प्रसिद्ध सूत्र निकाला है।
त्रिभुज का क्षेत्रफल - हीरोन के सूत्र द्वारा
We know that the area of triangle when its height is given, is × base × height. Now suppose that we know the lengths of the sides of a scalene triangle and not the height. How can we find its area ? For instance, you have a triangular park whose sides are m, m, and m. How will we calculate its area? Definitely if we want to apply the formula, we will have to calculate its height. But we do not have a clue to calculate
the height.
The formula given by Heron about the area of a triangle, is also known as Hero’s formula. It is stated as:
त्रिभुज का क्षेत्रफल =
जहाँ त्रिभुज की भुजाएँ हैं, और = अर्ध-परिधि, अर्थात, त्रिभुज की आधी परिधि
उदाहरण
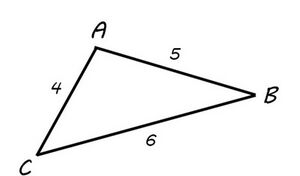
1.चित्र में दर्शाए गए त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
मान लीजिए
त्रिभुज का क्षेत्रफल=
=
=
=
= इकाइयाँ
2.एक त्रिभुजाकार भूखंड की भुजाएँ के अनुपात में हैं तथा इसका परिमाप मीटर है। इसका क्षेत्रफल ज्ञात कीजिए।
हल: मान लीजिए कि मीटर में भुजाएँ हैं
तब, हम जानते हैं कि त्रिभुज का परिमाप
अतः भुजाएँ मीटर में हैं
m
त्रिभुज का क्षेत्रफल =
=
=
= m2