त्रिभुज के गुण: Difference between revisions
(added content) |
(added content) |
||
| Line 29: | Line 29: | ||
Construct a bisector <math>AD</math> which meets the side <math>BC</math> at right angles. | Construct a bisector <math>AD</math> which meets the side <math>BC</math> at right angles. | ||
अब <math>\triangle BAD</math> और <math>\triangle CAD</math> में हमारे पास है, | |||
<math>\angle BAD =\angle CAD </math> ( | <math>\angle BAD =\angle CAD </math> (संरचना से) | ||
<math>AD=AD</math> ( | <math>AD=AD</math> (समान भुजाएँ) | ||
<math>\angle BDA =\angle CDA = 90^\circ </math> ( | <math>\angle BDA =\angle CDA = 90^\circ </math> (संरचना से) | ||
अत:, <math>\triangle BAD \cong \triangle CAD</math> (ASA सर्वांगसमता मानदंड द्वारा) | |||
इसलिए, <math>AB=AC</math> (CPCT द्वारा) | |||
अथवा <math>\triangle BCA</math> समद्विबाहु है। | |||
[[Category:त्रिभुज]][[Category:कक्षा-9]][[Category:गणित]] | [[Category:त्रिभुज]][[Category:कक्षा-9]][[Category:गणित]] | ||
Revision as of 10:52, 18 September 2024
प्रमेय 1: समद्विबाहु त्रिभुज की समान भुजाओं के सम्मुख कोण समान होते हैं
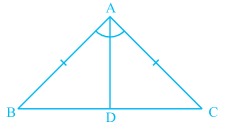
प्रमाण: चित्र 1 में दिखाए गए समद्विबाहु त्रिभुज पर विचार करें, जहाँ है।
हमें यह सिद्ध करना होगा कि भुजाओं और के सम्मुख कोण समान अर्थात् हैं।
हम पहले का एक समद्विभाजक बनाते हैं और इसे नाम देते हैं।
अब और में हमारे पास है,
(दिया हुआ)
(संरचना से)
(दोनों में समान)
अत:, (SAS सर्वांगसमता मानदंड द्वारा)
इसलिए, (CPCT द्वारा)
अतः सिद्ध हुआ।
Theorem 2: The sides opposite to equal angles of a triangle are equal.
Proof: In a triangle shown in fig 1, base angles are equal and we need to prove that or is an isosceles triangle.
Construct a bisector which meets the side at right angles.
अब और में हमारे पास है,
(संरचना से)
(समान भुजाएँ)
(संरचना से)
अत:, (ASA सर्वांगसमता मानदंड द्वारा)
इसलिए, (CPCT द्वारा)
अथवा समद्विबाहु है।