समांतर श्रेढ़ी: Difference between revisions
(added content) |
(added content) |
||
| Line 1: | Line 1: | ||
समांतर श्रेढ़ी (AP) एक [[अनुक्रम]] है जहाँ प्रत्येक दो क्रमिक पदों के बीच का अंतर समान होता है। उदाहरण के लिए, अनुक्रम <math>2, 6, 10, 14, ...</math> एक समांतर श्रेढ़ी (AP) है क्योंकि यह एक प्रतिरूप का अनुसरण करता है जहाँ प्रत्येक संख्या पिछले पद में <math>4</math> जोड़कर प्राप्त की जाती है। AP का एक वास्तविक जीवन उदाहरण एक कर्मचारी की वार्षिक आय द्वारा गठित अनुक्रम है जिसकी आय हर साल $5000 की एक निश्चित राशि से बढ़ती है। | समांतर श्रेढ़ी (AP) एक [[अनुक्रम]] है जहाँ प्रत्येक दो क्रमिक पदों के बीच का अंतर समान होता है। उदाहरण के लिए, अनुक्रम <math>2, 6, 10, 14, ...</math> एक समांतर श्रेढ़ी (AP) है क्योंकि यह एक प्रतिरूप का अनुसरण करता है जहाँ प्रत्येक संख्या पिछले पद में <math>4</math> जोड़कर प्राप्त की जाती है। AP का एक वास्तविक जीवन उदाहरण एक कर्मचारी की वार्षिक आय द्वारा गठित अनुक्रम है जिसकी आय हर साल $5000 की एक निश्चित राशि से बढ़ती है। | ||
इस लेख में, हम समांतर श्रेढ़ी की अवधारणा, इसके <math>n</math>वें पद, | इस लेख में, हम समांतर श्रेढ़ी की अवधारणा, इसके <math>n</math>वें पद, सार्व अंतर और AP के <math>n</math> पदों के योग को खोजने के लिए AP सूत्रों का पता लगाएंगे। हम अवधारणा की बेहतर समझ के लिए समांतर श्रेढ़ी सूत्र के आधार पर विभिन्न उदाहरणों को हल करेंगे। | ||
== परिभाषा == | == परिभाषा == | ||
समांतर श्रेढ़ी (AP) संख्याओं का एक क्रम है, जहाँ प्रत्येक दो क्रमिक पदों के बीच का अंतर समान होता है। इस श्रेढ़ी में, पहले पद को छोड़कर प्रत्येक पद, अपने पिछले पद में एक निश्चित संख्या जोड़कर प्राप्त किया जाता है। इस निश्चित संख्या को | समांतर श्रेढ़ी (AP) संख्याओं का एक क्रम है, जहाँ प्रत्येक दो क्रमिक पदों के बीच का अंतर समान होता है। इस श्रेढ़ी में, पहले पद को छोड़कर प्रत्येक पद, अपने पिछले पद में एक निश्चित संख्या जोड़कर प्राप्त किया जाता है। इस निश्चित संख्या को सार्व अंतर के रूप में जाना जाता है और इसे 'd' द्वारा दर्शाया जाता है। समांतर श्रेढ़ी के पहले पद को आमतौर पर '<math>a</math>' या '<math>a_1 </math>' द्वारा दर्शाया जाता है। | ||
उदाहरण के लिए, <math>1, 5, 9, 13, 17, 21, 25, 29, 33, ...</math>एक समांतर श्रेढ़ी है क्योंकि प्रत्येक दो क्रमिक पदों के बीच का अंतर समान (जैसे <math>4</math>) होता है। यानी,<math>5 - 1 = 9 - 5 = 13 - 9 = 17 - 13 = 21 - 17 = 25 - 21 = 29 - 25 = 33 - 29 = ... = 4</math>। हम यह भी देख सकते हैं कि इस AP का प्रत्येक पद (पहले पद को छोड़कर) अपने पिछले पद में <math>4</math> जोड़कर प्राप्त किया जाता है। इस समांतर श्रेढ़ी में: | उदाहरण के लिए, <math>1, 5, 9, 13, 17, 21, 25, 29, 33, ...</math>एक समांतर श्रेढ़ी है क्योंकि प्रत्येक दो क्रमिक पदों के बीच का अंतर समान (जैसे <math>4</math>) होता है। यानी,<math>5 - 1 = 9 - 5 = 13 - 9 = 17 - 13 = 21 - 17 = 25 - 21 = 29 - 25 = 33 - 29 = ... = 4</math>। हम यह भी देख सकते हैं कि इस AP का प्रत्येक पद (पहले पद को छोड़कर) अपने पिछले पद में <math>4</math> जोड़कर प्राप्त किया जाता है। इस समांतर श्रेढ़ी में: | ||
* <math>a = 1</math> (पहला पद) | * <math>a = 1</math> (पहला पद) | ||
* <math>d = 4</math> (पदों के बीच " | * <math>d = 4</math> (पदों के बीच "सार्व अंतर") | ||
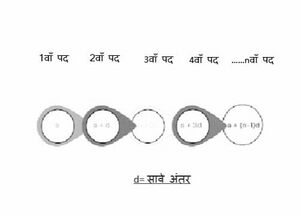
[[File:समांतर श्रेढ़ी.jpg|thumb|चित्र - समांतर श्रेढ़ी]]इस प्रकार, एक समांतर श्रेढ़ी, | [[File:समांतर श्रेढ़ी.jpg|thumb|चित्र - समांतर श्रेढ़ी]]इस प्रकार, एक समांतर श्रेढ़ी, सार्व रूप से, इस प्रकार लिखी जा सकती है:<math>\{a, a + d, a + 2d, a + 3d, ...\}</math> | ||
| Line 30: | Line 30: | ||
AP के <math>n</math> पदों का योग: <math>S_n = n/2 (2a + (n - 1) d) = n/2 (a + l)</math>, जहाँ <math>l</math> समांतर श्रेढ़ी का अंतिम पद है। | AP के <math>n</math> पदों का योग: <math>S_n = n/2 (2a + (n - 1) d) = n/2 (a + l)</math>, जहाँ <math>l</math> समांतर श्रेढ़ी का अंतिम पद है। | ||
== समांतर श्रेढ़ी में प्रयुक्त सामान्य शब्द == | == समांतर श्रेढ़ी में प्रयुक्त सामान्य शब्द == | ||
| Line 39: | Line 37: | ||
जैसा कि नाम से पता चलता है, AP का पहला पद श्रेढ़ी की पहली संख्या है। इसे आमतौर पर <math>a_1</math> (या) <math>a</math> द्वारा दर्शाया जाता है। उदाहरण के लिए, अनुक्रम <math>6, 13, 20, 27, 34, . . . .</math>में पहला पद <math>6</math> है। यानी, <math>a_1 = 6</math> (या) <math>a = 6</math>। | जैसा कि नाम से पता चलता है, AP का पहला पद श्रेढ़ी की पहली संख्या है। इसे आमतौर पर <math>a_1</math> (या) <math>a</math> द्वारा दर्शाया जाता है। उदाहरण के लिए, अनुक्रम <math>6, 13, 20, 27, 34, . . . .</math>में पहला पद <math>6</math> है। यानी, <math>a_1 = 6</math> (या) <math>a = 6</math>। | ||
=== समांतर श्रेढ़ी का | === समांतर श्रेढ़ी का सार्व अंतर === | ||
हम जानते हैं कि AP एक ऐसा अनुक्रम है जहाँ पहले पद को छोड़कर प्रत्येक पद अपने पिछले पद में एक निश्चित संख्या जोड़कर प्राप्त किया जाता है। यहाँ, "निश्चित संख्या" को " | हम जानते हैं कि AP एक ऐसा अनुक्रम है जहाँ पहले पद को छोड़कर प्रत्येक पद अपने पिछले पद में एक निश्चित संख्या जोड़कर प्राप्त किया जाता है। यहाँ, "निश्चित संख्या" को "सार्व अंतर" कहा जाता है और इसे '<math>d</math>' द्वारा दर्शाया जाता है, अर्थात, यदि पहला पद <math>a_1</math> है, तो: दूसरा पद <math>a_1+ d</math> है, तीसरा पद <math>a_1+ d + d = a_1 + 2d</math> है, और चौथा पद <math>a_1 + 2d + d = a_1+ 3d</math> है और इसी तरह आगे भी। उदाहरण के लिए, अनुक्रम <math>6, 13, 20, 27, 34,. . .</math>में, पहले पद को छोड़कर प्रत्येक पद, अपने पिछले पद में <math>7</math> जोड़कर प्राप्त किया जाता है। इस प्रकार, सार्व अंतर है, <math>d=7</math>। सामान्य तौर पर, सार्व अंतर एक AP के प्रत्येक दो क्रमिक पदों के बीच का अंतर होता है। इस प्रकार, AP के सार्व अंतर की गणना करने का सूत्र है: <math>d = a_n - a_n</math><sub>-1</sub>। | ||
यहाँ उनके पहले पद और | यहाँ उनके पहले पद और सार्व अंतर के साथ कुछ AP उदाहरण दिए गए हैं। | ||
* <math>6, 13, 20, 27, 34, . . . .</math> एक AP है जिसका पहला पद <math>6</math> है और सार्व अंतर <math>7</math> है। | * <math>6, 13, 20, 27, 34, . . . .</math> एक AP है जिसका पहला पद <math>6</math> है और सार्व अंतर <math>7</math> है। | ||
| Line 59: | Line 57: | ||
* AP संख्याओं की एक सूची है जिसमें प्रत्येक पद पूर्ववर्ती संख्या में एक निश्चित संख्या जोड़कर प्राप्त किया जाता है। | * AP संख्याओं की एक सूची है जिसमें प्रत्येक पद पूर्ववर्ती संख्या में एक निश्चित संख्या जोड़कर प्राप्त किया जाता है। | ||
* <math>a </math> को पहले पद के रूप में दर्शाया जाता है, <math>d</math> एक | * <math>a </math> को पहले पद के रूप में दर्शाया जाता है, <math>d</math> एक सार्व अंतर है, <math>a_n</math> को <math>n</math>वाँ पद और <math>n</math> को पदों की संख्या के रूप में दर्शाया जाता है। | ||
* सामान्य रूप से, AP को <math>a, a + d, a + 2d, a + 3d, ...</math> के रूप में दर्शाया जा सकता है। | * सामान्य रूप से, AP को <math>a, a + d, a + 2d, a + 3d, ...</math> के रूप में दर्शाया जा सकता है। | ||
* AP का <math>n</math>वाँ पद <math>a_n = a + (n-1)d</math> द्वारा प्राप्त किया जा सकता है। | * AP का <math>n</math>वाँ पद <math>a_n = a + (n-1)d</math> द्वारा प्राप्त किया जा सकता है। | ||
* AP का योग <math>s_n= n/2 [2a + (n-1) d]</math> द्वारा प्राप्त किया जा सकता है। | * AP का योग <math>s_n= n/2 [2a + (n-1) d]</math> द्वारा प्राप्त किया जा सकता है। | ||
* AP का ग्राफ एक सीधी रेखा है जिसमें ढलान | * AP का ग्राफ एक सीधी रेखा है जिसमें ढलान सार्व अंतर है। | ||
* | * सार्व अंतर हमेशा सकारात्मक होने की आवश्यकता नहीं है। उदाहरण के लिए, प्रगति में,<math>16, 8, 0, -8, -16, ...</math> सार्व अंतर ऋणात्मक है <math>(d = 8-16 = 0-8 = -8-0 = -16 -(-8) =... = -8)</math>। | ||
[[Category:अनुक्रम तथा श्रेणी]][[Category:कक्षा-11]][[Category:गणित]] | [[Category:अनुक्रम तथा श्रेणी]][[Category:कक्षा-11]][[Category:गणित]] | ||
Latest revision as of 15:05, 18 November 2024
समांतर श्रेढ़ी (AP) एक अनुक्रम है जहाँ प्रत्येक दो क्रमिक पदों के बीच का अंतर समान होता है। उदाहरण के लिए, अनुक्रम एक समांतर श्रेढ़ी (AP) है क्योंकि यह एक प्रतिरूप का अनुसरण करता है जहाँ प्रत्येक संख्या पिछले पद में जोड़कर प्राप्त की जाती है। AP का एक वास्तविक जीवन उदाहरण एक कर्मचारी की वार्षिक आय द्वारा गठित अनुक्रम है जिसकी आय हर साल $5000 की एक निश्चित राशि से बढ़ती है।
इस लेख में, हम समांतर श्रेढ़ी की अवधारणा, इसके वें पद, सार्व अंतर और AP के पदों के योग को खोजने के लिए AP सूत्रों का पता लगाएंगे। हम अवधारणा की बेहतर समझ के लिए समांतर श्रेढ़ी सूत्र के आधार पर विभिन्न उदाहरणों को हल करेंगे।
परिभाषा
समांतर श्रेढ़ी (AP) संख्याओं का एक क्रम है, जहाँ प्रत्येक दो क्रमिक पदों के बीच का अंतर समान होता है। इस श्रेढ़ी में, पहले पद को छोड़कर प्रत्येक पद, अपने पिछले पद में एक निश्चित संख्या जोड़कर प्राप्त किया जाता है। इस निश्चित संख्या को सार्व अंतर के रूप में जाना जाता है और इसे 'd' द्वारा दर्शाया जाता है। समांतर श्रेढ़ी के पहले पद को आमतौर पर '' या '' द्वारा दर्शाया जाता है।
उदाहरण के लिए, एक समांतर श्रेढ़ी है क्योंकि प्रत्येक दो क्रमिक पदों के बीच का अंतर समान (जैसे ) होता है। यानी,। हम यह भी देख सकते हैं कि इस AP का प्रत्येक पद (पहले पद को छोड़कर) अपने पिछले पद में जोड़कर प्राप्त किया जाता है। इस समांतर श्रेढ़ी में:
- (पहला पद)
- (पदों के बीच "सार्व अंतर")
इस प्रकार, एक समांतर श्रेढ़ी, सार्व रूप से, इस प्रकार लिखी जा सकती है:
उपरोक्त उदाहरण में हमारे पास है:
समांतर श्रेढ़ी सूत्र
AP के पहले पद '' और सार्व अंतर '' के लिए, नीचे समांतर श्रेढ़ी सूत्रों की एक सूची दी गई है, जिनका उपयोग प्रायः AP से संबंधित विभिन्न समस्याओं को हल करने के लिए किया जाता है:
AP का सार्व अंतर: -1
AP का वाँ पद:
AP के पदों का योग: , जहाँ समांतर श्रेढ़ी का अंतिम पद है।
समांतर श्रेढ़ी में प्रयुक्त सामान्य शब्द
अब से, हम समांतर श्रेढ़ी को AP के रूप में संक्षिप्त करेंगे। AP को साधारणतः इस प्रकार दर्शाया जाता है:इसमें निम्नलिखित शब्दावली उपस्थित है।
समांतर श्रेढ़ी का पहला पद
जैसा कि नाम से पता चलता है, AP का पहला पद श्रेढ़ी की पहली संख्या है। इसे आमतौर पर (या) द्वारा दर्शाया जाता है। उदाहरण के लिए, अनुक्रम में पहला पद है। यानी, (या) ।
समांतर श्रेढ़ी का सार्व अंतर
हम जानते हैं कि AP एक ऐसा अनुक्रम है जहाँ पहले पद को छोड़कर प्रत्येक पद अपने पिछले पद में एक निश्चित संख्या जोड़कर प्राप्त किया जाता है। यहाँ, "निश्चित संख्या" को "सार्व अंतर" कहा जाता है और इसे '' द्वारा दर्शाया जाता है, अर्थात, यदि पहला पद है, तो: दूसरा पद है, तीसरा पद है, और चौथा पद है और इसी तरह आगे भी। उदाहरण के लिए, अनुक्रम में, पहले पद को छोड़कर प्रत्येक पद, अपने पिछले पद में जोड़कर प्राप्त किया जाता है। इस प्रकार, सार्व अंतर है, । सामान्य तौर पर, सार्व अंतर एक AP के प्रत्येक दो क्रमिक पदों के बीच का अंतर होता है। इस प्रकार, AP के सार्व अंतर की गणना करने का सूत्र है: -1।
यहाँ उनके पहले पद और सार्व अंतर के साथ कुछ AP उदाहरण दिए गए हैं।
- एक AP है जिसका पहला पद है और सार्व अंतर है।
- एक AP है जिसका पहला पद है और सार्व अंतर है।
- एक AP है जिसका पहला पद है और सार्व अंतर है।
- एक AP है जिसका पहला पद है और सार्व अंतर है।
समांतर श्रेढ़ी का योग
एक समांतर श्रेढ़ी (AP) पर विचार करें जिसका पहला पद (या) है और सार्व अंतर है।
जब वाँ पद ज्ञात न हो तो समांतर श्रेढ़ी के पहले पदों का योग होता है।
जब वाँ पद () ज्ञात हो तो समांतर श्रेढ़ी के पहले पदों का योग होता है।
महत्वपूर्ण टिप्पणियाँ
- AP संख्याओं की एक सूची है जिसमें प्रत्येक पद पूर्ववर्ती संख्या में एक निश्चित संख्या जोड़कर प्राप्त किया जाता है।
- को पहले पद के रूप में दर्शाया जाता है, एक सार्व अंतर है, को वाँ पद और को पदों की संख्या के रूप में दर्शाया जाता है।
- सामान्य रूप से, AP को के रूप में दर्शाया जा सकता है।
- AP का वाँ पद द्वारा प्राप्त किया जा सकता है।
- AP का योग द्वारा प्राप्त किया जा सकता है।
- AP का ग्राफ एक सीधी रेखा है जिसमें ढलान सार्व अंतर है।
- सार्व अंतर हमेशा सकारात्मक होने की आवश्यकता नहीं है। उदाहरण के लिए, प्रगति में, सार्व अंतर ऋणात्मक है ।