आंशिक भिन्नों द्वारा समाकलन

आंशिक भिन्नों द्वारा समाकलन एक ऐसी विधि है जिसका उपयोग किसी परिमेय भिन्न समाकलन को अपघटित करने और फिर समाकलित करने के लिए किया जाता है जिसके हर में जटिल पद होते हैं। आंशिक भिन्न का उपयोग करके, हम व्यंजक की गणना करते हैं और उसे सरल पदों में अपघटित करते हैं ताकि हम इस प्रकार प्राप्त व्यंजक की आसानी से गणना या समाकलन कर सकें।

आंशिक भिन्नों द्वारा समाकलन में मूल विचार हर को गुणनखंडित करना और फिर उन्हें दो अलग-अलग भिन्नों में अपघटित करना है जहाँ हर क्रमशः गुणनखंड होते हैं और अंश की गणना उपयुक्त रूप से की जाती है। आइए आंशिक भिन्नों द्वारा समाकलन में उपयोग किए जाने वाले विभिन्न रूपों और विभिन्न विधियों के बारे में अधिक जानें।

परिभाषा

आंशिक भिन्नों द्वारा समाकलन, समाकलन की तीन विधियों में से एक है। इस विधि में, हम उचित परिमेय भिन्न को सरल परिमेय भिन्नों के योग में अपघटित करते हैं। परिमेय भिन्न को सरल परिमेय भिन्नों में अपघटित करना सदैव संभव होता है और यह आंशिक भिन्न अपघटन नामक प्रक्रिया द्वारा किया जाता है।

आइए इसे एक उदाहरण की सहायता से समझते हैं। मान लीजिए हमारे पास $5/6$ है, तो हम इसे$5/6=1/2+1/3$ के रूप में अपघटित कर सकते हैं, इसी तरह, हम दो आंशिक भिन्नों को बीजगणितीय रूप से अपघटित करके ऐसा करते हैं। मान लीजिए हमारे पास है:

$2/(x+1)-1/x$

जोड़ने पर हमें प्राप्त होगा

$2/(x+1)-1/x=(x-1)/(x^{2}+x)$

अब यदि हमारे पास है

$(x-1)/(x^{2}+x)$

इसलिए हम इसे अपघटित कर सकते हैं

$(x-1)/(x^{2}+x)=2/(x+1)-1/x$

इस प्रकार आंशिक भिन्नों को सरल पदों में अपघटित कर दिया गया है। इसलिए अब परिणामी पदों को एकीकृत करना अपेक्षाकृत आसान कार्य होगा। आंशिक भिन्नों द्वारा समाकलन इस प्रकार होगा:

$\int [f(x)/g(x)]dx=\int [p(x)/q(x)]dx+\int [r(x)/s(x)]dx$

जहाँ

• $f(x)/g(x)=p(x)/q(x)+r(x)/s(x)$और
• $g(x)=q(x).s(x)$

आंशिक भिन्नों द्वारा समाकलन में प्रयुक्त रूप

आंशिक भिन्नों द्वारा समाकलन

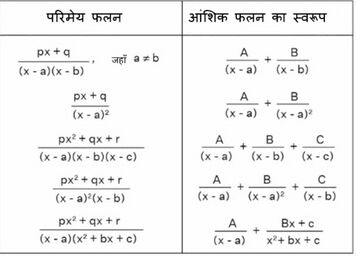
आंशिक भिन्नों द्वारा समाकलन में, हम उचित परिमेय भिन्नों के विशिष्ट रूपों को अपघटित करने के लिए कुछ विशेष प्रकार की आंशिक भिन्नों का उपयोग कर सकते हैं। इन रूपों का उपयोग करके हम आसानी से उन भिन्नों को समाकलित कर सकते हैं जो निम्न तालिका में दिए गए समान रूपों में हैं।

आंशिक भिन्नों द्वारा समाकलन की विधि

आंशिक भिन्नों द्वारा समाकलन की विधि एक सरल प्रक्रिया है। आइए आंशिक भिन्नों द्वारा समाकलन की विधि को एक उदाहरण से समझें। हमारे पास है:

$\int [6/(x^{2}-1)]dx$

चूँकि हम जानते हैं: $x^{2}-1=(x+1)(x-1)$

अतः हम लिख सकते हैं:

$\int [6/(x^{2}-1)]dx=\int [6/(x+1)(x-1)]dx$

अब इस प्रकार के परिमेय रूप के लिए आंशिक भिन्न के रूप का उपयोग करने पर, हमें प्राप्त होता है:

$6/(x+1)(x-1)=A/(x-1)+B/(x+1)$

अब, हमें $A$ और $B$ का मान ज्ञात करना है, जिससे दोनों पक्षों पर एक समान हर बन जाए।

$6/(x+1)(x-1)=[A/(x-1)][(x+1)/(x+1)]+[B/(x+1)][(x-1)/(x-1)]$

$6/(x+1)(x-1)=[A(x+1)+B(x-1)]/(x-1)(x+1)$

इसके अलावा, दोनों पक्षों के हर बराबर हैं, इसलिए अंश भी बराबर होंगे।

$6=[A(x+1)+B(x-1)]$

हल करने पर हमें प्राप्त होता है,

$A=3,$ और $B=-3$

अत: हम लिख सकते हैं

$6/(x+1)(x-1)=3/(x-1)+(-3)/(x+1)$

अब, हम लिख सकते हैं:

$\int [6/(x^{2}-1)]dx=\int [3/(x-1)-3/(x+1)]dx$

हल करने पर, हमें प्राप्त होगा:

$\int [6/(x^{2}-1)]dx=-3\ln(\left\vert x+1\right\vert )+3\ln(\left\vert x-1\right\vert )+C$

उदाहरण

उदाहरण:

आंशिक भिन्नो द्वारा समाकलज का उपयोग करके समाकलन करें: $\int [x+1]/x(1+xe^{x})^{2}dx$

समाधान: ध्यान दें कि $xe^{x}$ का व्युत्पन्न $(x+1)e^{x}$ है। इस प्रकार, हम $xe^{x}$ को एक नए चर $t$ के लिए प्रतिस्थापित कर सकते हैं यदि हम उपरोक्त अभिव्यक्ति के अंश और हर को $e^{x}$ से गुणा करते हैं:

$I=\int [x+1]/x(1+xe^{x})^{2}dx$

$=\int (x+1)ex/xe^{x}(1+xe^{x})^{2}dx$

प्रतिस्थापन $xe^{x}=t$ अब $I$ को घटाकर निम्न कर देता है:

$I=\int dt/(t(1+t)^{2}).dt$

अब हम आंशिक भिन्नों का उपयोग करके इस व्यंजक को $t$ में विस्तारित कर सकते हैं:

$1/(t(1+t)^{2})=A/t+B/(1+t)+C/(1+t)^{2}$

$\Rightarrow 1=A(1+t)^{2}+B(1+t)t+Ct$

$t=0\Rightarrow A=1$ रखने पर

$t=-1\Rightarrow C=-1$ रखने पर

$t^{2}\Rightarrow 0=A+B$ के गुणांक की तुलना करें

$\Rightarrow B=-1$

आंशिक भिन्न का विस्तार है:

$1/t-1/(1+t)-1/(1+t)^{2}$

इसलिए, $I$ इस प्रकार है

$I=\ln \left\vert t\right\vert -\ln \left\vert 1+t\right\vert +1/(1+t)+C$

उत्तर: $\int [x+1]/x(1+xe^{2})^{2}dx=\ln \left\vert t\right\vert -\ln \left\vert \right\vert +1/(1+xe^{x})+C$