सदिश योग का त्रिभुज नियम: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
इन दो नियमों का उपयोग करके, हम यह प्रमाणित करने जा रहे हैं कि दो [[सदिशों का योगफल|सदिशों का योग]] उन्हें शीर्ष से अन्त्य तक जोड़कर प्राप्त किया जाता है और सदिश योग उस सदिश द्वारा दिया जाता है जो मुक्त अन्त्य और मुक्त शीर्ष को जोड़ता है। आइए आने वाले अनुभागों में इनमें से प्रत्येक नियम का विस्तार से अध्ययन करें। | इन दो नियमों का उपयोग करके, हम यह प्रमाणित करने जा रहे हैं कि दो [[सदिशों का योगफल|सदिशों का योग]] उन्हें शीर्ष से अन्त्य तक जोड़कर प्राप्त किया जाता है और सदिश योग उस सदिश द्वारा दिया जाता है जो मुक्त अन्त्य और मुक्त शीर्ष को जोड़ता है। आइए आने वाले अनुभागों में इनमें से प्रत्येक नियम का विस्तार से अध्ययन करें। | ||
सदिश योग का त्रिभुज नियम एक गणितीय अवधारणा है जिसका उपयोग दो सदिशों का योग ज्ञात करने के लिए किया जाता है। इस नियम का उपयोग दो सदिशों को जोड़ने के लिए किया जाता है जब पहले सदिश के शीर्ष को दूसरे सदिश की अन्त्य से जोड़ा जाता है और फिर पहले सदिश की अन्त्य को दूसरे सदिश के शीर्ष से जोड़कर एक त्रिभुज बनाया जाता है, और इस प्रकार परिणामी योग सदिश प्राप्त किया जाता है। इसीलिए सदिश योग के त्रिभुज नियम को सदिशों के योग के लिए शीर्ष से अन्त्य विधि भी कहा जाता है। | सदिश योग का त्रिभुज नियम एक गणितीय अवधारणा है जिसका उपयोग दो सदिशों का योग ज्ञात करने के लिए किया जाता है। इस नियम का उपयोग दो सदिशों को जोड़ने के लिए किया जाता है जब पहले सदिश के शीर्ष को दूसरे सदिश की अन्त्य से जोड़ा जाता है और फिर पहले सदिश की अन्त्य को दूसरे सदिश के शीर्ष से जोड़कर एक त्रिभुज बनाया जाता है, और इस प्रकार परिणामी योग सदिश प्राप्त किया जाता है। इसीलिए सदिश योग के त्रिभुज नियम को सदिशों के योग के लिए शीर्ष से अन्त्य विधि भी कहा जाता है। | ||
Latest revision as of 13:45, 11 December 2024
सदिश योग के दो नियम होते हैं ।
- त्रिभुज नियम
- समांतर चतुर्भुज नियम
इन दो नियमों का उपयोग करके, हम यह प्रमाणित करने जा रहे हैं कि दो सदिशों का योग उन्हें शीर्ष से अन्त्य तक जोड़कर प्राप्त किया जाता है और सदिश योग उस सदिश द्वारा दिया जाता है जो मुक्त अन्त्य और मुक्त शीर्ष को जोड़ता है। आइए आने वाले अनुभागों में इनमें से प्रत्येक नियम का विस्तार से अध्ययन करें।
सदिश योग का त्रिभुज नियम एक गणितीय अवधारणा है जिसका उपयोग दो सदिशों का योग ज्ञात करने के लिए किया जाता है। इस नियम का उपयोग दो सदिशों को जोड़ने के लिए किया जाता है जब पहले सदिश के शीर्ष को दूसरे सदिश की अन्त्य से जोड़ा जाता है और फिर पहले सदिश की अन्त्य को दूसरे सदिश के शीर्ष से जोड़कर एक त्रिभुज बनाया जाता है, और इस प्रकार परिणामी योग सदिश प्राप्त किया जाता है। इसीलिए सदिश योग के त्रिभुज नियम को सदिशों के योग के लिए शीर्ष से अन्त्य विधि भी कहा जाता है।
आइए हम सदिशों के योग के त्रिभुज नियम, इसके कथन, सूत्र और प्रमाण का अध्ययन करें। इस नियम का उपयोग शुद्ध विस्थापन, वेग, त्वरण आदि को निर्धारित करने के लिए किया जाता है।
परिभाषा
सदिश योग का त्रिभुज नियम, एक ऐसा नियम है जिसका उपयोग सदिश बीजगणित में दो या अधिक सदिशों को जोड़ने पर परिणामी योग सदिश निर्धारित करने के लिए किया जाता है। मान लीजिए हमारे पास एक कार है जो नीचे दिए गए चित्र में दिखाए अनुसार बिंदु से तक जा रही है। एक बार जब यह बिंदु पर पहुँच जाती है, तो यह बिंदु तक फिर से चलना प्रारंभ कर देती है। अब, कार के शुद्ध विस्थापन को निर्धारित करने के लिए, हम सदिश जोड़ की अवधारणा का उपयोग करते हैं। कार का शुद्ध विस्थापन सदिश द्वारा दिया जाता है जिसे सदिश जोड़ के त्रिभुज नियम का उपयोग करके इस प्रकार से परिकलित किया जा सकता है:
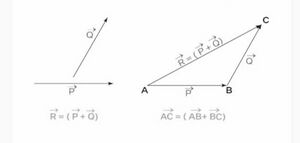
इसी प्रकार, यदि हमारे पास नीचे दिए गए अनुसार दो सदिश और हैं और हमें उनका योग ज्ञात करना है, तो हम सदिश को उसके परिमाण और दिशा को बदले बिना इस प्रकार घुमा सकते हैं कि उसकी अन्त्य सदिश के शीर्ष से जुड़ जाए। तब, सदिश योग के त्रिभुज नियम का उपयोग करते हुए सदिश और का योग इस प्रकार दिया जाता है,
सदिश योग के त्रिभुज नियम का सूत्र
दो सदिश और पर विचार करें जैसे कि उनके बीच का कोण है और सदिश योग के त्रिभुज नियम का उपयोग करते हुए उनका परिणामी योग सदिश सदिश द्वारा दिया गया है। सदिशों के योग के लिए त्रिभुज नियम का उपयोग करते हुए परिणामी सदिश के परिमाण और दिशा का सूत्र इस प्रकार दिया गया है,
सदिश योग के त्रिभुज नियम का प्रमाण
त्रिकोण नियम के प्रमाण पर जाने से पहले, आइए सबसे पहले सदिश योग के त्रिभुज नियम के कथन को देखें:
कथन: यदि किसी पिंड पर एक साथ कार्य करने वाले दो सदिशों को परिमाण और दिशा दोनों में त्रिभुज की दो भुजाओं द्वारा एक क्रम में दर्शाया जाता है, तो इन दो सदिशों का परिणामी योग सदिश (परिमाण और दिशा दोनों) उस त्रिभुज की तीसरी भुजा द्वारा दिया जाता है, जिसे विपरीत क्रम में लिया जाता है।
नीचे दी गई आकृति में, दो सदिश और पर विचार करें, जिनके परिमाण क्रमशः भुजाओं और द्वारा दिए गए हैं। अब, सदिश योग के त्रिभुज नियम का उपयोग करते हुए इन सदिशों का योग परिणामी सदिश (त्रिकोण की भुजा ) द्वारा दिया जाता है, जिसका परिमाण और दिशा है
अब, भुजा को बिंदु तक इस प्रकार बढ़ाएँ कि पर लंबवत हो और सदिश और के बीच का कोण हो। साथ ही, परिणामी सदिश की दिशा कोण द्वारा दी गई है। समकोण त्रिभुज में, हमारे पास है
समकोण त्रिभुज ABC में, हमारे पास है
और
और
और
(2) के मानों को (1) में प्रतिस्थापित करने पर, हमें प्राप्त होता है
→परिणामी सदिश का परिमाण
अब, की दिशा ज्ञात करने के लिए, हमारे पास समकोण त्रिभुज है,
[ (2) से]
[ (2) से]
→परिणामी सदिश की दिशा
इसलिए, हमने सदिश योग के त्रिभुज नियम के सूत्र सिद्ध कर दिए हैं।
महत्वपूर्ण टिप्पणियाँ
- सदिश योग के त्रिभुज नियम का उपयोग दो सदिशों का योग ज्ञात करने के लिए किया जाता है, जब पहले सदिश का शीर्ष दूसरे सदिश की अन्त्य से जुड़ जाता है।
- परिणामी योग सदिश का परिमाण:
- परिणामी सदिश की दिशा: