रैखिक प्रोग्रामन समस्याओं के भिन्न प्रकार: Difference between revisions
No edit summary |
(formulas) |
||
| Line 1: | Line 1: | ||
रैखिक | रैखिक प्रोग्रामन, जिसे एलपी(LP) के रूप में भी संक्षिप्त किया जाता है, एक सरल विधि है जिसका उपयोग रैखिक फलन का उपयोग करके जटिल वास्तविक दुनिया के संबंधों को दर्शाने के लिए किया जाता है। इस प्रकार प्राप्त गणितीय प्रतिरूप में तत्वों का एक दूसरे के साथ रैखिक संबंध होता है। रैखिक प्रोग्रामन का उपयोग रैखिक अनुकूलन करने के लिए किया जाता है ताकि सर्वोत्तम परिणाम प्राप्त किया जा सके। | ||
रैखिक | रैखिक प्रोग्रामन एक ऐसी प्रक्रिया है जिसका उपयोग रैखिक फलन के सर्वोत्तम परिणाम को निर्धारित करने के लिए किया जाता है। यह कुछ सरल धारणाएँ बनाकर रैखिक अनुकूलन करने का सबसे अच्छा उपाय है। रैखिक फलन को उद्देश्य फलन के रूप में जाना जाता है। वास्तविक दुनिया के संबंध बेहद जटिल हो सकते हैं। हालाँकि, रैखिक प्रोग्रामन का उपयोग ऐसे संबंधों को दर्शाने के लिए किया जा सकता है, जिससे उनका विश्लेषण करना आसान हो जाता है। | ||
रैखिक | रैखिक प्रोग्रामन का उपयोग ऊर्जा, दूरसंचार, परिवहन और विनिर्माण जैसे कई उद्योगों में किया जाता है। यह लेख रैखिक प्रोग्रामन के विभिन्न पहलुओं जैसे परिभाषा, और इस तकनीक का उपयोग करके समस्याओं को हल करने के तरीके और संबंधित रैखिक प्रोग्रामन उदाहरणों पर प्रकाश डालता है। | ||
== रैखिक | == रैखिक प्रोग्रामन परिभाषा == | ||
रैखिक | रैखिक प्रोग्रामन को एक ऐसी तकनीक के रूप में परिभाषित किया जा सकता है जिसका उपयोग किसी रैखिक फलन को अनुकूलित करने के लिए किया जाता है ताकि सर्वोत्तम परिणाम प्राप्त किया जा सके। इस रैखिक फलन या उद्देश्य फलन में रैखिक समानता और असमानता प्रतिबंध उपस्थित हैं। हम उद्देश्य फलन को न्यूनतम या अधिकतम करके सर्वोत्तम परिणाम प्राप्त करते हैं। | ||
== रैखिक | == रैखिक प्रोग्रामन समस्याओं का हल == | ||
रैखिक | रैखिक प्रोग्रामन समस्या को हल करने का सबसे महत्वपूर्ण भाग पहले दिए गए आकड़ों का उपयोग करके समस्या को तैयार करना है। रैखिक प्रोग्रामन समस्याओं को हल करने के चरण नीचे दिए गए हैं: | ||
* चरण 1: निर्णय चर की पहचान करें। | * चरण 1: निर्णय चर की पहचान करें। | ||
* चरण 2: उद्देश्य फलन | * चरण 2: उद्देश्य फलन व्यवस्थित करें। जाँच करें कि फलन को न्यूनतम या अधिकतम करने की आवश्यकता है या नहीं। | ||
* चरण 3: | * चरण 3: प्रतिबंधों को लिखें। | ||
* चरण 4: सुनिश्चित करें कि निर्णय चर 0 से अधिक या बराबर हैं। (गैर-नकारात्मक प्रतिबंध) | * चरण 4: सुनिश्चित करें कि निर्णय चर <math>0 </math> से अधिक या बराबर हैं। (गैर-नकारात्मक प्रतिबंध) | ||
* चरण 5: | * चरण 5: संकेतन या आलेखीय विधि का उपयोग करके रैखिक प्रोग्रामन समस्या को हल करें। | ||
आइए हम निम्नलिखित अनुभागों में इन विधियों के बारे में विस्तार से अध्ययन करें। | आइए हम निम्नलिखित अनुभागों में इन विधियों के बारे में विस्तार से अध्ययन करें। | ||
== रैखिक | == रैखिक प्रोग्रामन विधियाँ == | ||
रैखिक | रैखिक प्रोग्रामन समस्या को हल करने के लिए दो मुख्य विधियाँ उपलब्ध हैं। ये हैं संकेतन विधि और आलेखीय विधि। नीचे दोनों विधियों का उपयोग करके रैखिक प्रोग्रामन समस्या को हल करने के चरण दिए गए हैं। | ||
सिंप्लेक्स विधि द्वारा रैखिक | === संकेतन(सिंप्लेक्स) विधि द्वारा रैखिक प्रोग्रामन === | ||
रैखिक प्रोग्रामन में संकेतन विधि को दो या अधिक निर्णय चर वाली समस्याओं पर लागू किया जा सकता है। मान लीजिए कि उद्देश्य फलन <math>Z = 40x_1 + 30x_2</math> को अधिकतम करने की आवश्यकता है और प्रतिबंध इस प्रकार दिए गए हैं: | |||
<math>x_1 + x_2 \leq 12</math> | |||
<math>2x_1 + x_2 \leq 16</math> | |||
<math>x_1 \geq 0, x_2 \geq 0</math> | |||
चरण 1: असमानताओं को समीकरणों में बदलने के लिए एक और चर जोड़ें, जिसे स्लैक चर के रूप में जाना जाता है। इसके अलावा, उद्देश्य फलन को समीकरण के रूप में फिर से लिखें। | चरण 1: असमानताओं को समीकरणों में बदलने के लिए एक और चर जोड़ें, जिसे स्लैक चर के रूप में जाना जाता है। इसके अलावा, उद्देश्य फलन को समीकरण के रूप में फिर से लिखें। | ||
| Line 42: | Line 41: | ||
y1 and y2 are the slack variables. | y1 and y2 are the slack variables. | ||
चरण 2: प्रारंभिक | चरण 2: प्रारंभिक संकेतन आव्यूह का निर्माण निम्नानुसार करें: | ||
चरण 3: सबसे ज़्यादा नकारात्मक प्रविष्टि वाले | चरण 3: सबसे ज़्यादा नकारात्मक प्रविष्टि वाले स्तम्भ की पहचान करें। इसे पिवट स्तम्भ कहा जाता है। चूँकि -40 सबसे ज़्यादा नकारात्मक प्रविष्टि है, इसलिए स्तम्भ 1 पिवट स्तम्भ होगा। | ||
चरण 4: सबसे दाएँ | चरण 4: सबसे दाएँ स्तम्भ की प्रविष्टियों को पिवट स्तम्भ की प्रविष्टियों से विभाजित करें। हम सबसे नीचे वाली पंक्ति की प्रविष्टियों को बाहर कर देते हैं। | ||
12 / 1 = 12 | 12 / 1 = 12 | ||
| Line 54: | Line 53: | ||
16 / 2 = 8 | 16 / 2 = 8 | ||
पिवट पंक्ति प्राप्त करने के लिए सबसे छोटे भागफल वाली पंक्ति की पहचान की जाती है। चूँकि 8, 12 की तुलना में छोटा भागफल है, इसलिए पंक्ति 2 पिवट पंक्ति बन जाती है। पिवट पंक्ति और पिवट | पिवट पंक्ति प्राप्त करने के लिए सबसे छोटे भागफल वाली पंक्ति की पहचान की जाती है। चूँकि 8, 12 की तुलना में छोटा भागफल है, इसलिए पंक्ति 2 पिवट पंक्ति बन जाती है। पिवट पंक्ति और पिवट स्तम्भ का प्रतिच्छेदन पिवट तत्व देता है। | ||
इस प्रकार, पिवट तत्व = 2. | इस प्रकार, पिवट तत्व = 2. | ||
चरण 5: पिवट तत्व की सहायता से | चरण 5: पिवट तत्व की सहायता से आव्यूह गुणों का उपयोग करके पिवटिंग करें, ताकि पिवट स्तम्भ में अन्य सभी प्रविष्टियाँ 0 हो जाएँ। | ||
प्राथमिक संचालन का उपयोग करके पंक्ति 2 को 2 से विभाजित करें (R2 / 2) | प्राथमिक संचालन का उपयोग करके पंक्ति 2 को 2 से विभाजित करें (R2 / 2) | ||
| Line 67: | Line 66: | ||
चरण 6: जाँच करें कि क्या सबसे नीचे वाली पंक्ति में नकारात्मक प्रविष्टियाँ हैं। यदि नहीं, तो इष्टतम समाधान निर्धारित किया गया है। यदि हाँ, तो चरण 3 पर वापस जाएँ और प्रक्रिया को दोहराएँ। -10 | |||
चरण 6: जाँच करें कि क्या सबसे नीचे वाली पंक्ति में नकारात्मक प्रविष्टियाँ हैं। यदि नहीं, तो इष्टतम समाधान निर्धारित किया गया है। यदि हाँ, तो चरण 3 पर वापस जाएँ और प्रक्रिया को दोहराएँ। -10 आव्यूह में एक नकारात्मक प्रविष्टि है, इसलिए, प्रक्रिया को दोहराना आवश्यक है। हमें निम्नलिखित आव्यूह मिलता है। | |||
| Line 76: | Line 76: | ||
साथ ही, जब x1 = 4 और x2 = 8 हो तो Z का मान = 400 | साथ ही, जब x1 = 4 और x2 = 8 हो तो Z का मान = 400 | ||
इस प्रकार, x1 = 4 और x2 = 8 इष्टतम बिंदु हैं और हमारी रैखिक | इस प्रकार, x1 = 4 और x2 = 8 इष्टतम बिंदु हैं और हमारी रैखिक प्रोग्रामन समस्या का समाधान है। | ||
== | == आलेखीय विधि द्वारा रैखिक प्रोग्रामन == | ||
यदि किसी रैखिक | यदि किसी रैखिक प्रोग्रामन समस्या में दो निर्णय चर हैं, तो ऐसी समस्या को हल करने के लिए आलेखीय विधि का उपयोग आसानी से किया जा सकता है। | ||
मान लीजिए हमें <math>Z = 2x + 5y</math> को अधिकतम करना है। | मान लीजिए हमें <math>Z = 2x + 5y</math> को अधिकतम करना है। | ||
| Line 87: | Line 87: | ||
where, x ≥ 0 and y ≥ 0. | where, x ≥ 0 and y ≥ 0. | ||
इस समस्या को | इस समस्या को आलेखीय विधि का उपयोग करके हल करने के लिए निम्नलिखित चरण हैं। | ||
चरण 1: सभी असमानता | चरण 1: सभी असमानता प्रतिबंधों को समीकरणों के रूप में लिखें। | ||
x + 4y = 24 | x + 4y = 24 | ||
| Line 114: | Line 114: | ||
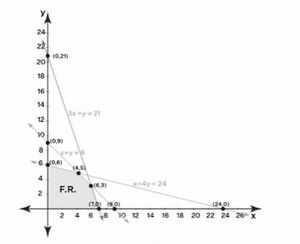
व्यवहार्य क्षेत्र को OABCD द्वारा दर्शाया जाता है क्योंकि यह उपर्युक्त तीनों प्रतिबंधों को संतुष्ट करता है। | व्यवहार्य क्षेत्र को OABCD द्वारा दर्शाया जाता है क्योंकि यह उपर्युक्त तीनों प्रतिबंधों को संतुष्ट करता है। | ||
[[File:आलेखीय विधि द्वारा रैखिक प्रोग्रामन.jpg|thumb|आलेखीय विधि द्वारा रैखिक प्रोग्रामन]] | |||
चरण 4: कोने के बिंदुओं के निर्देशांक निर्धारित करें। कोने के बिंदु संभव क्षेत्र के शीर्ष हैं। | चरण 4: कोने के बिंदुओं के निर्देशांक निर्धारित करें। कोने के बिंदु संभव क्षेत्र के शीर्ष हैं। | ||
| Line 126: | Line 126: | ||
D = (0, 6) | D = (0, 6) | ||
चरण 5: उद्देश्य फलन में प्रत्येक कोने बिंदु को प्रतिस्थापित करें। वह बिंदु जो उद्देश्य फलन का सबसे बड़ा (अधिकतम) या सबसे छोटा (न्यूनतम) मान देता है, वह इष्टतम बिंदु होगा। | चरण 5: उद्देश्य फलन में प्रत्येक कोने बिंदु को प्रतिस्थापित करें। वह बिंदु जो उद्देश्य फलन का सबसे बड़ा (अधिकतम) या सबसे छोटा (न्यूनतम) मान देता है, वह इष्टतम बिंदु होगा। | ||
Revision as of 13:38, 16 December 2024
रैखिक प्रोग्रामन, जिसे एलपी(LP) के रूप में भी संक्षिप्त किया जाता है, एक सरल विधि है जिसका उपयोग रैखिक फलन का उपयोग करके जटिल वास्तविक दुनिया के संबंधों को दर्शाने के लिए किया जाता है। इस प्रकार प्राप्त गणितीय प्रतिरूप में तत्वों का एक दूसरे के साथ रैखिक संबंध होता है। रैखिक प्रोग्रामन का उपयोग रैखिक अनुकूलन करने के लिए किया जाता है ताकि सर्वोत्तम परिणाम प्राप्त किया जा सके।
रैखिक प्रोग्रामन एक ऐसी प्रक्रिया है जिसका उपयोग रैखिक फलन के सर्वोत्तम परिणाम को निर्धारित करने के लिए किया जाता है। यह कुछ सरल धारणाएँ बनाकर रैखिक अनुकूलन करने का सबसे अच्छा उपाय है। रैखिक फलन को उद्देश्य फलन के रूप में जाना जाता है। वास्तविक दुनिया के संबंध बेहद जटिल हो सकते हैं। हालाँकि, रैखिक प्रोग्रामन का उपयोग ऐसे संबंधों को दर्शाने के लिए किया जा सकता है, जिससे उनका विश्लेषण करना आसान हो जाता है।
रैखिक प्रोग्रामन का उपयोग ऊर्जा, दूरसंचार, परिवहन और विनिर्माण जैसे कई उद्योगों में किया जाता है। यह लेख रैखिक प्रोग्रामन के विभिन्न पहलुओं जैसे परिभाषा, और इस तकनीक का उपयोग करके समस्याओं को हल करने के तरीके और संबंधित रैखिक प्रोग्रामन उदाहरणों पर प्रकाश डालता है।
रैखिक प्रोग्रामन परिभाषा
रैखिक प्रोग्रामन को एक ऐसी तकनीक के रूप में परिभाषित किया जा सकता है जिसका उपयोग किसी रैखिक फलन को अनुकूलित करने के लिए किया जाता है ताकि सर्वोत्तम परिणाम प्राप्त किया जा सके। इस रैखिक फलन या उद्देश्य फलन में रैखिक समानता और असमानता प्रतिबंध उपस्थित हैं। हम उद्देश्य फलन को न्यूनतम या अधिकतम करके सर्वोत्तम परिणाम प्राप्त करते हैं।
रैखिक प्रोग्रामन समस्याओं का हल
रैखिक प्रोग्रामन समस्या को हल करने का सबसे महत्वपूर्ण भाग पहले दिए गए आकड़ों का उपयोग करके समस्या को तैयार करना है। रैखिक प्रोग्रामन समस्याओं को हल करने के चरण नीचे दिए गए हैं:
- चरण 1: निर्णय चर की पहचान करें।
- चरण 2: उद्देश्य फलन व्यवस्थित करें। जाँच करें कि फलन को न्यूनतम या अधिकतम करने की आवश्यकता है या नहीं।
- चरण 3: प्रतिबंधों को लिखें।
- चरण 4: सुनिश्चित करें कि निर्णय चर से अधिक या बराबर हैं। (गैर-नकारात्मक प्रतिबंध)
- चरण 5: संकेतन या आलेखीय विधि का उपयोग करके रैखिक प्रोग्रामन समस्या को हल करें।
आइए हम निम्नलिखित अनुभागों में इन विधियों के बारे में विस्तार से अध्ययन करें।
रैखिक प्रोग्रामन विधियाँ
रैखिक प्रोग्रामन समस्या को हल करने के लिए दो मुख्य विधियाँ उपलब्ध हैं। ये हैं संकेतन विधि और आलेखीय विधि। नीचे दोनों विधियों का उपयोग करके रैखिक प्रोग्रामन समस्या को हल करने के चरण दिए गए हैं।
संकेतन(सिंप्लेक्स) विधि द्वारा रैखिक प्रोग्रामन
रैखिक प्रोग्रामन में संकेतन विधि को दो या अधिक निर्णय चर वाली समस्याओं पर लागू किया जा सकता है। मान लीजिए कि उद्देश्य फलन को अधिकतम करने की आवश्यकता है और प्रतिबंध इस प्रकार दिए गए हैं:
चरण 1: असमानताओं को समीकरणों में बदलने के लिए एक और चर जोड़ें, जिसे स्लैक चर के रूप में जाना जाता है। इसके अलावा, उद्देश्य फलन को समीकरण के रूप में फिर से लिखें।
- 40x1 - 30x2 + Z = 0
x1 + x2 + y1 =12
2x1 + x2 + y2 =16
y1 and y2 are the slack variables.
चरण 2: प्रारंभिक संकेतन आव्यूह का निर्माण निम्नानुसार करें:
चरण 3: सबसे ज़्यादा नकारात्मक प्रविष्टि वाले स्तम्भ की पहचान करें। इसे पिवट स्तम्भ कहा जाता है। चूँकि -40 सबसे ज़्यादा नकारात्मक प्रविष्टि है, इसलिए स्तम्भ 1 पिवट स्तम्भ होगा।
चरण 4: सबसे दाएँ स्तम्भ की प्रविष्टियों को पिवट स्तम्भ की प्रविष्टियों से विभाजित करें। हम सबसे नीचे वाली पंक्ति की प्रविष्टियों को बाहर कर देते हैं।
12 / 1 = 12
16 / 2 = 8
पिवट पंक्ति प्राप्त करने के लिए सबसे छोटे भागफल वाली पंक्ति की पहचान की जाती है। चूँकि 8, 12 की तुलना में छोटा भागफल है, इसलिए पंक्ति 2 पिवट पंक्ति बन जाती है। पिवट पंक्ति और पिवट स्तम्भ का प्रतिच्छेदन पिवट तत्व देता है।
इस प्रकार, पिवट तत्व = 2.
चरण 5: पिवट तत्व की सहायता से आव्यूह गुणों का उपयोग करके पिवटिंग करें, ताकि पिवट स्तम्भ में अन्य सभी प्रविष्टियाँ 0 हो जाएँ।
प्राथमिक संचालन का उपयोग करके पंक्ति 2 को 2 से विभाजित करें (R2 / 2)
चरण 6: जाँच करें कि क्या सबसे नीचे वाली पंक्ति में नकारात्मक प्रविष्टियाँ हैं। यदि नहीं, तो इष्टतम समाधान निर्धारित किया गया है। यदि हाँ, तो चरण 3 पर वापस जाएँ और प्रक्रिया को दोहराएँ। -10 आव्यूह में एक नकारात्मक प्रविष्टि है, इसलिए, प्रक्रिया को दोहराना आवश्यक है। हमें निम्नलिखित आव्यूह मिलता है।
नीचे की पंक्ति को समीकरण के रूप में लिखने पर हमें Z = 400 - 20
y1 - 10y2 मिलता है। इस प्रकार, 400 वह उच्चतम मान है जिसे Z तब प्राप्त कर सकता है जब y1 और y2 दोनों 0 हों।
साथ ही, जब x1 = 4 और x2 = 8 हो तो Z का मान = 400
इस प्रकार, x1 = 4 और x2 = 8 इष्टतम बिंदु हैं और हमारी रैखिक प्रोग्रामन समस्या का समाधान है।
आलेखीय विधि द्वारा रैखिक प्रोग्रामन
यदि किसी रैखिक प्रोग्रामन समस्या में दो निर्णय चर हैं, तो ऐसी समस्या को हल करने के लिए आलेखीय विधि का उपयोग आसानी से किया जा सकता है।
मान लीजिए हमें को अधिकतम करना है।
The constraints are x + 4y ≤ 24, 3x + y ≤ 21 and x + y ≤ 9
where, x ≥ 0 and y ≥ 0.
इस समस्या को आलेखीय विधि का उपयोग करके हल करने के लिए निम्नलिखित चरण हैं।
चरण 1: सभी असमानता प्रतिबंधों को समीकरणों के रूप में लिखें।
x + 4y = 24
3x + y = 21
x + y = 9
चरण 2: परीक्षण बिंदुओं की पहचान करके इन रेखाओं को ग्राफ पर अंकित करें।
x + 4y = 24 एक रेखा है जो (0, 6) और (24, 0) से होकर गुजरती है। [x = 0 प्रतिस्थापित करने पर बिंदु (0, 6) प्राप्त होता है। इसी प्रकार, जब y = 0 होता है तो बिंदु (24, 0) निर्धारित होता है।]
3x + y = 21 passes through (0, 21) and (7, 0).
x + y = 9 passes through (9, 0) and (0, 9).
चरण 3: व्यवहार्य क्षेत्र की पहचान करें। व्यवहार्य क्षेत्र को उस क्षेत्र के रूप में परिभाषित किया जा सकता है जो निर्देशांकों के एक समूह से घिरा होता है जो असमानताओं की कुछ विशेष प्रणाली को संतुष्ट कर सकता है।
कोई भी बिंदु जो रेखा x + 4y = 24 पर या उसके नीचे स्थित है, वह x + 4y ≤ 24 की बाध्यता को संतुष्ट करेगा।
इसी तरह, 3x + y = 21 पर या उसके नीचे स्थित एक बिंदु 3x + y ≤ 21 को संतुष्ट करता है।
साथ ही, रेखा x + y = 9 पर या उसके नीचे स्थित एक बिंदु x + y ≤ 9 को संतुष्ट करता है।
व्यवहार्य क्षेत्र को OABCD द्वारा दर्शाया जाता है क्योंकि यह उपर्युक्त तीनों प्रतिबंधों को संतुष्ट करता है।
चरण 4: कोने के बिंदुओं के निर्देशांक निर्धारित करें। कोने के बिंदु संभव क्षेत्र के शीर्ष हैं।
O = (0, 0)
A = (7, 0)
B = (6, 3)। B दो रेखाओं 3x + y = 21 और x + y = 9 का प्रतिच्छेद बिंदु है। इस प्रकार, 3x + y = 21 में y = 9 - x प्रतिस्थापित करके हम प्रतिच्छेद बिंदु निर्धारित कर सकते हैं।
C = (4, 5) x + 4y = 24 और x + y = 9 के प्रतिच्छेद द्वारा गठित
D = (0, 6)
चरण 5: उद्देश्य फलन में प्रत्येक कोने बिंदु को प्रतिस्थापित करें। वह बिंदु जो उद्देश्य फलन का सबसे बड़ा (अधिकतम) या सबसे छोटा (न्यूनतम) मान देता है, वह इष्टतम बिंदु होगा।
| कोने बिंदु | |
| O = (0, 0) | 0 |
| A = (7, 0) | 14 |
| B = (6, 3) | 27 |
| C = (4, 5) | 33 |
| D = (0, 6) | 30 |
का अधिकतम मान है और यह पर होता है। इस प्रकार, हल और है।