दूरी-सूत्र: Difference between revisions
(added content) |
(content added) |
||
| Line 21: | Line 21: | ||
</math> हैं। | </math> हैं। | ||
[[File:Distance Formula.jpg|alt=Fig 1 - Distance Formula|none|thumb|500x500px|Fig 1 - Distance Formula]] | [[File:Distance Formula.jpg|alt=Fig 1 - Distance Formula|none|thumb|500x500px|Fig 1 - Distance Formula]] | ||
फिर दो बिंदुओं के बीच की दूरी ज्ञात करने का सूत्र <math>AB</math> द्वारा दिया गया है | |||
</math> | |||
<math>AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2 } | <math>AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2 } | ||
Revision as of 09:43, 19 June 2024
निर्देशांक ज्यामिति में दूरी सूत्र का उपयोग समतल में दो बिंदुओं के बीच की दूरी ज्ञात करने के लिए किया जाता है। अक्ष से किसी बिंदु की दूरी को उसका निर्देशांक या भुज कहते हैं। अक्ष से किसी बिंदु की दूरी को उसका निर्देशांक या कोटि कहते हैं। अक्ष पर किसी बिंदु के निर्देशांक के रूप के होते हैं, और अक्ष पर किसी बिंदु के निर्देशांक के रूप के होते हैं। किसी समतल में किसी भी दो बिंदुओं के बीच की दूरी ज्ञात करने के लिए, हम पाइथागोरस प्रमेय का उपयोग करेंगे।
दूरी-सूत्र क्या है?
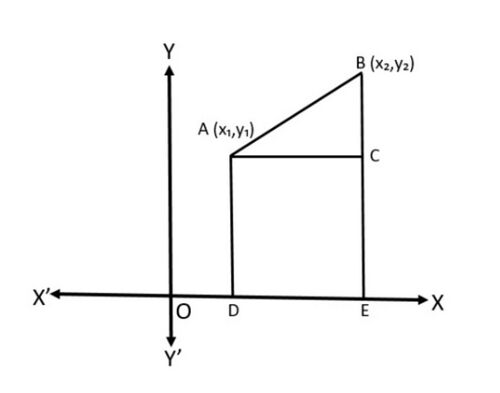
दूरी सूत्र वह सूत्र है, जिसका उपयोग किसी भी दो बिंदुओं के बीच की दूरी ज्ञात करने के लिए किया जाता है, केवल तभी जब निर्देशांक हमें ज्ञात हों। ये निर्देशांक अक्ष या अक्ष या दोनों पर स्थित हो सकते हैं। मान लीजिए, एक समतल में दो बिंदु, मान लीजिए और हैं (चित्र 1 देखें) बिंदु के निर्देशांक हैं और के हैं।
फिर दो बिंदुओं के बीच की दूरी ज्ञात करने का सूत्र द्वारा दिया गया है
दूरी-सूत्र व्युत्पत्ति
Let us find the distance between two points and shown Fig.1
Draw and perpendicular to the axis. A perpendicular from the point on is drawn to meet it at the point .
Then, , . So, . Also, , . Hence
Now, applying the Pythagoras theorem in , we get
is the distance formula.
Example
Find the distance between the two points and
Solution:
Let
Distance between the two points and