एक लम्ब वृत्तीय शंकु का पृष्ठीय क्षेत्रफल: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
Surface area of a cone is the total area covered by its surface. The total surface area will cover the base area and lateral surface area of the cone. Cone is defined as a three-dimensional solid structure that has a circular base. A cone can be viewed as a set of non-congruent circular disks that are placed over one another such that the ratio of the radius of adjacent disks remains constant. | |||
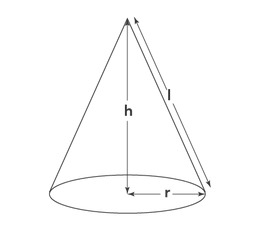
[[File:Right Circular Cone.jpg|alt=Fig.1 Right Circular Cone|none|thumb|Fig.1 Right Circular Cone]] | |||
Right circular cone shown in Fig. 1 has a vertex at the top, <math>r</math> the base radius , <math>h</math> the height of the cone and <math>l</math> the slant height of the cone. | |||
'''Curved Surface Area of a Cone''' = <math>\frac{1}{2}\times l \times 2\pi r=\pi rl</math> | |||
Here <math>r</math> the base radius , <math>l</math> the slant height of the cone. | |||
Also <math>l^2=r^2+h^2</math> by applying Pythagoras Theorem. Here <math>h</math> is the height of the cone. | |||
Therefore, <math>l=\sqrt{r^2+h^2}</math> | |||
'''Total Surface Area of a Cone''' = <math>\pi rl +\pi r^2=\pi r(l+r) | |||
</math> | |||
== Examples == | |||
1. Find the curved surface area and the total surface area of a right circular cone whose slant height is <math>10</math> cm and base radius is <math>7</math> cm. | |||
Solution: | |||
Curved surface area = <math>\pi rl</math> | |||
= <math>\frac{22}{7}\times 7 \times 10= 220</math> cm<sup>2</sup> | |||
Total surface area = <math>\pi r(l+r)</math> | |||
=<math>\frac{22}{7}\times 7 \times (10+7)=374</math> cm<sup>2</sup> | |||
[[Category:पृष्ठीय क्षेत्रफल और आयतन]] | [[Category:पृष्ठीय क्षेत्रफल और आयतन]] | ||
[[Category:गणित]] | [[Category:गणित]] | ||
[[Category:कक्षा-9]] | [[Category:कक्षा-9]] | ||
Revision as of 10:25, 10 September 2024
Surface area of a cone is the total area covered by its surface. The total surface area will cover the base area and lateral surface area of the cone. Cone is defined as a three-dimensional solid structure that has a circular base. A cone can be viewed as a set of non-congruent circular disks that are placed over one another such that the ratio of the radius of adjacent disks remains constant.
Right circular cone shown in Fig. 1 has a vertex at the top, the base radius , the height of the cone and the slant height of the cone.
Curved Surface Area of a Cone =
Here the base radius , the slant height of the cone.
Also by applying Pythagoras Theorem. Here is the height of the cone.
Therefore,
Total Surface Area of a Cone =
Examples
1. Find the curved surface area and the total surface area of a right circular cone whose slant height is cm and base radius is cm.
Solution:
Curved surface area =
= cm2
Total surface area =
= cm2