त्रिभुज के गुण: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
Theorem 1: Angles opposite to equal sides of an isosceles triangle are equal | |||
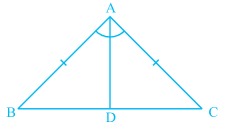
[[File:Isosceles Triangle -1.jpg|alt=Fig 1 - Isosceles triangle|none|thumb|Fig 1 - Isosceles triangle]] | |||
Proof: Consider an isosceles triangle <math>BCA</math> shown in fig 1 where <math>AB=AC</math>. | |||
We need to prove that the angles opposite to the sides <math>AB</math> and <math>AC</math> are equal, that is, <math>\angle ABC = \angle ACB</math> | |||
We first draw a bisector of <math>\angle BAC</math> and name it as <math>AD</math>. | |||
Now in <math>\triangle BAD</math> and <math>\triangle CAD</math> we have, | |||
<math>AB=AC</math> (Given) | |||
<math>\angle BAD =\angle CAD </math> (By construction) | |||
<math>AD=AD</math> (Common to both) | |||
Thus, <math>\triangle BAD \cong \triangle CAD</math> (By SAS congruence criterion) | |||
So, <math>\angle ABC =\angle ACB </math> (By CPCT) | |||
Hence proved. | |||
Theorem 2: The sides opposite to equal angles of a triangle are equal. | |||
Proof: In a triangle <math>BCA</math> shown in fig 1, base angles are equal and we need to prove that <math>AB=AC</math> or <math>BCA</math> is an isosceles triangle. | |||
Construct a bisector <math>AD</math> which meets the side <math>BC</math> at right angles. | |||
Now in <math>\triangle BAD</math> and <math>\triangle CAD</math> we have, | |||
<math>\angle BAD =\angle CAD </math> (By construction) | |||
<math>AD=AD</math> (Common side) | |||
<math>\angle BDA =\angle CDA = 90^\circ </math> (By construction) | |||
Thus, <math>\triangle BAD \cong \triangle CAD</math> (By ASA congruence criterion) | |||
So, <math>AB=AC</math> (By CPCT) | |||
Or <math>\triangle BCA</math> is isosceles. | |||
[[Category:त्रिभुज]][[Category:कक्षा-9]][[Category:गणित]] | [[Category:त्रिभुज]][[Category:कक्षा-9]][[Category:गणित]] | ||
Revision as of 10:04, 18 September 2024
Theorem 1: Angles opposite to equal sides of an isosceles triangle are equal
Proof: Consider an isosceles triangle shown in fig 1 where .
We need to prove that the angles opposite to the sides and are equal, that is,
We first draw a bisector of and name it as .
Now in and we have,
(Given)
(By construction)
(Common to both)
Thus, (By SAS congruence criterion)
So, (By CPCT)
Hence proved.
Theorem 2: The sides opposite to equal angles of a triangle are equal.
Proof: In a triangle shown in fig 1, base angles are equal and we need to prove that or is an isosceles triangle.
Construct a bisector which meets the side at right angles.
Now in and we have,
(By construction)
(Common side)
(By construction)
Thus, (By ASA congruence criterion)
So, (By CPCT)
Or is isosceles.