केंद्र से जीवा पर लंब: Difference between revisions
(added content) |
(added content) |
||
| Line 1: | Line 1: | ||
गणित में, जीवा एक रेखा खंड है जो एक वृत्त की परिधि पर दो बिंदुओं को जोड़ती है। हम जानते हैं कि किसी वृत्त की सबसे लंबी जीवा वह व्यास होती है जो वृत्त के केंद्र से होकर गुजरती है। इस लेख में वृत्त के केन्द्र से | गणित में, जीवा एक रेखा खंड है जो एक वृत्त की परिधि पर दो बिंदुओं को जोड़ती है। हम जानते हैं कि किसी वृत्त की सबसे लंबी जीवा वह व्यास होती है जो वृत्त के केंद्र से होकर गुजरती है। इस लेख में वृत्त के केन्द्र से लंब से सम्बंधित प्रमेय और उसके प्रमाण तथा इस प्रमेय के व्युत्क्रम पर विस्तार से चर्चा की गई है। | ||
== | == केंद्र से जीवा पर लंब– प्रमेय एवं प्रमाण == | ||
=== | === प्रमेय : === | ||
The perpendicular from the centre of a circle to a chord bisects the chord. | The perpendicular from the centre of a circle to a chord bisects the chord. | ||
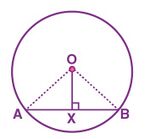
''' | '''प्रमाण:'''[[File:Circle-1.jpg|alt=Fig. 1|thumb|150x150px|Fig. 1]] | ||
Consider a circle with centre <math>O</math> shown in Fig. 1 | Consider a circle with centre <math>O</math> shown in Fig. 1 | ||
| Line 31: | Line 31: | ||
Thus, the perpendicular from the centre of a circle to a chord bisects the chord, is proved. | Thus, the perpendicular from the centre of a circle to a chord bisects the chord, is proved. | ||
=== | === इस प्रमेय का व्युत्क्रम: === | ||
The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord | The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord | ||
''' | '''प्रमाण:''' | ||
Consider the Fig. 1 | Consider the Fig. 1 | ||
Revision as of 11:25, 18 September 2024
गणित में, जीवा एक रेखा खंड है जो एक वृत्त की परिधि पर दो बिंदुओं को जोड़ती है। हम जानते हैं कि किसी वृत्त की सबसे लंबी जीवा वह व्यास होती है जो वृत्त के केंद्र से होकर गुजरती है। इस लेख में वृत्त के केन्द्र से लंब से सम्बंधित प्रमेय और उसके प्रमाण तथा इस प्रमेय के व्युत्क्रम पर विस्तार से चर्चा की गई है।
केंद्र से जीवा पर लंब– प्रमेय एवं प्रमाण
प्रमेय :
The perpendicular from the centre of a circle to a chord bisects the chord.
प्रमाण:
Consider a circle with centre shown in Fig. 1
is a chord such that the line is perpendicular to the chord . ()
We need to prove:
Consider two triangles and
(Common side)
(Radii)
By using the RHS rule, we can prove that the triangle is congruent to .
Therefore,
Hence, we can say that ( Using CPCT)
Thus, the perpendicular from the centre of a circle to a chord bisects the chord, is proved.
इस प्रमेय का व्युत्क्रम:
The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord
प्रमाण:
Consider the Fig. 1
Assume that is the chord of a circle with centre .
The centre is joined to the midpoint of the chord .
Now, we need to prove
Join and and the two triangles formed are and .
Here,
(Radii)
(Common side)
(As, is the midpoint of AB)
Therefore, we can say that .
Thus, by using the RHS rule, we get
This proves that the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.Hence, the converse of this theorem is proved.