कैसेग्रेन दूरदर्शक: Difference between revisions

Listen

Latest revision as of 12:21, 23 September 2024

cassegrain telescope

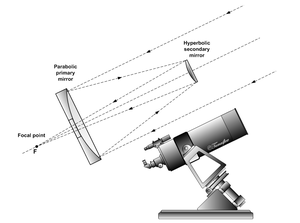
कैससेग्रेन टेलीस्कोप एक प्रकार का परावर्तक टेलीस्कोप है जिसका उपयोग अंतरिक्ष में दूर की वस्तुओं, जैसे तारे, ग्रह और आकाशगंगाओं का निरीक्षण करने के लिए किया जाता है। इसे लेंस के इतर दर्पण का उपयोग करके प्रकाश को पकड़ने और केंद्रित करने के लिए डिज़ाइन किया गया है, जो इसे खगोल विज्ञान के लिए आदर्श बनाता है। दूरदर्शक का नाम इसके आविष्कारक लॉरेंट कैसग्रेन के नाम पर रखा गया है।

कैससेग्रेन टेलीस्कोप के घटक

कैससेग्रेन टेलीस्कोप में प्रकाश पथ

प्राथमिक दर्पण (अवतल दर्पण)

प्राथमिक दर्पण दूरदर्शक के नीचे एक बड़ा अवतल दर्पण होता है। यह दूर की वस्तुओं से प्रकाश को एकत्रित और परावर्तित करता है।

द्वितीयक दर्पण (उत्तल दर्पण)

दूरदर्शक के शीर्ष के समीप लटका हुआ, द्वितीयक दर्पण प्राथमिक दर्पण में एक छेद के माध्यम से प्रकाश को वापस नीचे की ओर परावर्तित करता है।

फोकल बिंदु

प्राथमिक और द्वितीयक दर्पणों के संयुक्त प्रभाव से प्रकाश किरणें प्राथमिक दर्पण के पीछे एक बिंदु पर एकत्रित हो जाती हैं। इस बिंदु को केंद्र बिंदु कहा जाता है।प्राथमिक और द्वितीयक दर्पणों के संयुक्त प्रभाव से प्रकाश किरणें प्राथमिक दर्पण के पीछे एक बिंदु पर एकत्रित हो जाती हैं। इस बिंदु को केंद्र बिंदु कहा जाता है।

कैससेग्रेन टेलीस्कोप के कार्य का सिद्धांत

प्रकाश संग्रह

जब दूर की वस्तु से प्रकाश दूरदर्शक में प्रवेश करता है, तो यह प्राथमिक दर्पण से टकराता है। दर्पण प्रकाश को परावर्तित करता है और उसे द्वितीयक दर्पण की ओर केंद्रित करता है।

द्वितीयक परावर्तन

द्वितीयक दर्पण आने वाली रोशनी को प्राथमिक दर्पण में एक छेद के माध्यम से वापस परावर्तित करता है। यह प्रतिबिंब प्रकाश को प्राथमिक दर्पण के पीछे केंद्र बिंदु की ओर एकत्रित करने का कारण बनता है।

ऑय-पीस या कैमरा

केंद्रित छवि का निरीक्षण करने के लिए, ऑय-पीस या कैमरा को फोकल बिंदु पर रखा जाता है।यह वह स्थान है, जहां जिस वस्तु का अवलोकन कीया जा रहा है, उसका विस्तार और विस्तृत दृश्य देखा जा सकता है।

गणितीय समीकरण

कैससेग्रेन टेलीस्कोप में संमलित ,गणितीय समीकरण मुख्य रूप से दर्पण के आकार और फोकल लंबाई से संबंधित हैं।

1. दर्पण समीकरण:

अवतल दर्पण (प्राथमिक दर्पण) के लिए दर्पण समीकरण वस्तु दूरी ( $d_{0}$ ), छवि दूरी ( $d_{i}$ ), और दर्पण की फोकल लंबाई ( $f$ ) से संबंधित है:

$f_{1}={\frac {1}{d_{o}}}+{\frac {1}{d_{i}}}$

2. आवर्धन समीकरण:

दूरदर्शक का आवर्धन ( $M$ ) छवि की ऊंचाई और वस्तु की ऊंचाई का अनुपात है। छोटे कोणों के लिए, इसे दो दर्पणों की फोकल लंबाई के अनुपात के रूप में अनुमानित किया जा सकता है:

$f=-{\frac {f_{objective}}{f_{eyepiece}}}$

जहां $f_{objective}$ प्राथमिक दर्पण की फोकल लंबाई है और $f_{eyepiece}$ , ऑय-पीस की फोकल लंबाई है।

संक्षेप में

ये समीकरण खगोलविदों और दूरदर्शक को अभिकल्पित करने वालों (डिजाइनरों) को यह समझने में सुविधा होती है कि दूरदर्शक के भीतर प्रकाश कैसे केंद्रित, आवर्धित और निर्देशित होता है, जिससे उन्हें ब्रह्मांड की खोज के लिए सटीक और शक्तिशाली अवलोकन उपकरण बनाने की अनुमति मिलती है।

@@ Line 6: / Line 6: @@
 [[File:Cassegrain.en.png|thumb|कैससेग्रेन टेलीस्कोप में प्रकाश पथ]]
-======    प्राथमिक दर्पण (अवतल दर्पण) ======
+====== '''प्राथमिक दर्पण (अवतल दर्पण)''' ======
 प्राथमिक दर्पण दूरदर्शक के नीचे एक बड़ा अवतल दर्पण होता है। यह दूर की वस्तुओं से प्रकाश को एकत्रित और परावर्तित करता है।
-======    द्वितीयक दर्पण (उत्तल दर्पण) ======
+====== '''द्वितीयक दर्पण (उत्तल दर्पण)''' ======
 दूरदर्शक के शीर्ष के समीप लटका हुआ, द्वितीयक दर्पण प्राथमिक दर्पण में एक छेद के माध्यम से प्रकाश को वापस नीचे की ओर परावर्तित करता है।
-======    फोकल बिंदु ======
+====== '''फोकल बिंदु''' ======
 प्राथमिक और द्वितीयक दर्पणों के संयुक्त प्रभाव से प्रकाश किरणें प्राथमिक दर्पण के पीछे एक बिंदु पर एकत्रित हो जाती हैं। इस बिंदु को केंद्र बिंदु कहा जाता है।प्राथमिक और द्वितीयक दर्पणों के संयुक्त प्रभाव से प्रकाश किरणें प्राथमिक दर्पण के पीछे एक बिंदु पर एकत्रित हो जाती हैं। इस बिंदु को केंद्र बिंदु कहा जाता है।
 == कैससेग्रेन टेलीस्कोप के कार्य का सिद्धांत ==
-======    प्रकाश संग्रह ======
+====== '''प्रकाश संग्रह''' ======
 जब दूर की वस्तु से प्रकाश दूरदर्शक में प्रवेश करता है, तो यह प्राथमिक दर्पण से टकराता है। दर्पण प्रकाश को परावर्तित करता है और उसे द्वितीयक दर्पण की ओर केंद्रित करता है।
-======    द्वितीयक परावर्तन ======
+======  '''द्वितीयक परावर्तन''' ======
 द्वितीयक दर्पण आने वाली रोशनी को प्राथमिक दर्पण में एक छेद के माध्यम से वापस परावर्तित करता है। यह प्रतिबिंब प्रकाश को प्राथमिक दर्पण के पीछे केंद्र बिंदु की ओर एकत्रित करने का कारण बनता है।
-======    ऑय-पीस या कैमरा ======
+====== '''ऑय-पीस या कैमरा''' ======
 केंद्रित छवि का निरीक्षण करने के लिए, ऑय-पीस या कैमरा को फोकल बिंदु पर रखा जाता है।यह वह स्थान है, जहां जिस वस्तु का अवलोकन कीया जा रहा है, उसका विस्तार और विस्तृत दृश्य देखा जा सकता है।
@@ Line 29: / Line 29: @@
 कैससेग्रेन टेलीस्कोप में संमलित ,गणितीय समीकरण मुख्य रूप से दर्पण के आकार और फोकल लंबाई से संबंधित हैं।
-. दर्पण समीकरण:
+'''1. दर्पण समीकरण:'''
 अवतल दर्पण (प्राथमिक दर्पण) के लिए दर्पण समीकरण वस्तु दूरी (<math>d_0 </math>), छवि दूरी (<math>d_i </math>), और दर्पण की फोकल लंबाई (<math>f</math>) से संबंधित है:
@@ Line 35: / Line 35: @@
 <math>f_1=\frac{1}{d_o}+\frac{1}{d_i} </math>
-. आवर्धन समीकरण:
+'''2. आवर्धन समीकरण:'''
 दूरदर्शक का आवर्धन (<math>M</math>) छवि की ऊंचाई और वस्तु की ऊंचाई का अनुपात है। छोटे कोणों के लिए, इसे दो दर्पणों की फोकल लंबाई के अनुपात के रूप में अनुमानित किया जा सकता है: