कोण-कोण समरूपता कसौटी

The Angle-Angle (AA) criterion for similarity of two triangles states that “If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar”.

The AA criterion states that if two angles of a triangle are respectively equal to the two angles of another triangle, we can prove that the third angle will also be equal on both the triangles. This can be done with the help of the angle sum property of a triangle.

Example

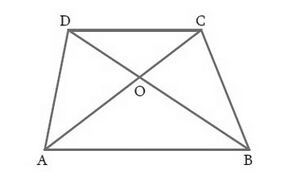
1.Diagonals $AC$ and $BD$ of a trapezium $ABCD$ with $AB\parallel DC$ intersect each other at the point $O$. Using a similarity criterion for two triangles, show that ${\frac {OA}{OC}}={\frac {OB}{OD}}$

Solution:

Let's draw a trapezium $ABCD$ with $AB\parallel DC$

If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.

This is referred to as AA similarity criterion for two triangles.

In $\triangle AOB$ and $\triangle COD$

$\angle AOB=\angle COD$ (vertically opposite angles)

$\angle BAO=\angle DCO$ (alternate interior angles)

Hence $\triangle AOB\sim \triangle COD$ (AA similarity criterion)

Hence ${\frac {OA}{OC}}={\frac {OB}{OD}}$