|
|
| Line 1: |
Line 1: |
| [[Category:त्रिकोणमिति के कुछ अनुप्रयोग]] | | [[Category:त्रिकोणमिति का परिचय]] |
| [[Category:गणित]] | | [[Category:गणित]] |
| [[Category:कक्षा-10]] | | [[Category:कक्षा-10]] |
Revision as of 20:20, 26 September 2024
त्रिकोणमितीय सर्वसमिकाएँ, त्रिकोणमिति का एक मूलभूत पहलू है, जो त्रिभुजों के कोणों और भुजाओं के बीच संबंधों का अध्ययन है। यह सर्वसमिकाएँ गणितीय समीकरण हैं जिनमें ज्या(साइन), कोटिज्या(कोसाइन) और स्पर्शरेखा जैसे त्रिकोणमितीय फलन उपस्थित होते हैं और उपस्थित चर के सभी मानों के लिए सत्य होते हैं।
त्रिकोणमितीय सर्वसमिकाएँ, व्यंजक को सरल बनाने, समीकरणों को हल करने और विज्ञान और इंजीनियरिंग के विभिन्न क्षेत्रों में गणितीय प्रमेयों को सिद्ध करने के लिए उपयोगी हैं। गणित, भौतिकी और इंजीनियरिंग जैसे क्षेत्रों में छात्रों और पेशेवरों(प्रोफेशनल्स) के लिए इन सर्वसमिकाएँ के गुणों और अनुप्रयोगों को समझना आवश्यक है।
पायथागॉरियन त्रिकोणमितीय सर्वसमिकाएँ
त्रिकोणमिति में पाइथागोरस त्रिकोणमितीय सर्वसमिकाएँ पाइथागोरस प्रमेय से ली गई हैं। निम्नलिखित 3 पाइथागोरस त्रिकोणमितीय सर्वसमिकाएँ हैं।



 में
में  पर समकोण है (चित्र-1 देखें) हमारे पास है
पर समकोण है (चित्र-1 देखें) हमारे पास है
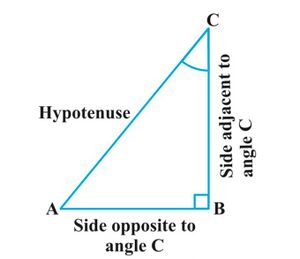
चित्र-1 त्रिकोणमितीय सर्वसमिकाएँ

 के प्रत्येक पद को
के प्रत्येक पद को  से विभाजित करने पर
से विभाजित करने पर

![{\displaystyle \left[{\frac {AB}{AC}}\right]^{2}+\left[{\frac {BC}{AC}}\right]^{2}=\left[{\frac {AC}{AC}}\right]^{2}}](/index.php?title=Special:MathShowImage&hash=5a23d7eb023eb05bf368edccf394f449&mode=mathml)

यह सभी  के लिए सत्य है जैसे कि
के लिए सत्य है जैसे कि 
(1) के प्रत्येक पद को  से विभाजित करने पर
से विभाजित करने पर

![{\displaystyle \left[{\frac {AB}{AB}}\right]^{2}+\left[{\frac {BC}{AB}}\right]^{2}=\left[{\frac {AC}{AB}}\right]^{2}}](/index.php?title=Special:MathShowImage&hash=9ef6b517375b118186cd5bdf40658795&mode=mathml)

यह सभी  के लिए सत्य है जैसे कि
के लिए सत्य है जैसे कि 
(1) के प्रत्येक पद को  से विभाजित करने पर
से विभाजित करने पर

![{\displaystyle \left[{\frac {AB}{BC}}\right]^{2}+\left[{\frac {BC}{BC}}\right]^{2}=\left[{\frac {AC}{BC}}\right]^{2}}](/index.php?title=Special:MathShowImage&hash=945ab876ba7df72a6b38620e8803138b&mode=mathml)

यह सभी  के लिए सत्य है जैसे कि
के लिए सत्य है जैसे कि 
