त्रिज्यखंड और वृत्तखंड के क्षेत्रेफल: Difference between revisions
(added the category) |
Ramamurthy (talk | contribs) (→उदाहरण) |
||
| Line 82: | Line 82: | ||
</math> cm<sup>2</sup> | </math> cm<sup>2</sup> | ||
[[Category:वृत्तों से संबंधित क्षेत्रफल]] | [[Category:वृत्तों से संबंधित क्षेत्रफल]] | ||
[[Category:गणित]] | |||
[[Category:कक्षा-10]] | [[Category:कक्षा-10]] | ||
Latest revision as of 20:23, 26 September 2024
त्रिज्यखंड
किसी वृत्त की दो त्रिज्याओं के बीच का वृत्ताकार क्षेत्र और उनके बीच का चाप वृत्त का त्रिज्यखंड कहलाता है। त्रिज्यखंड सदैव वृत्त के केंद्र से प्रारंभ होता है। अर्धवृत्त को वृत्त का त्रिज्यखंड भी कहा जाता है।
त्रिज्यखंड दो प्रकार के होते हैं, लघु त्रिज्यखंड और दीर्घ त्रिज्यखंड।
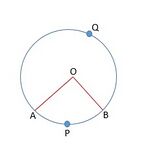
चित्र 1 में , केंद्र सहित वृत्त का एक त्रिज्यखंड है। को त्रिज्यखंड का कोण कहा जाता है। को लघु त्रिज्यखंड कहा जाता है और को दीर्घ त्रिज्यखंड कहा जाता है।
दीर्घ त्रिज्यखंड का कोण है।
वृत्तखंड
किसी जीवा और संगत चाप के बीच घिरे वृत्ताकार क्षेत्र के भाग को वृत्त का खंड कहा जाता है।
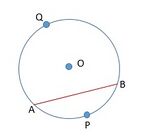
चित्र 2 में केंद्र वाले वृत्त की एक जीवा है।
वृत्त का एक खंड है।
खंड दो प्रकार के होते हैं, लघु वृत्तखंड और दीर्घ वृत्तखंड ।
को लघु वृत्तखंड कहा जाता है और
को दीर्घ वृत्तखंड कहा जाता है।
त्रिज्यखंड का क्षेत्रफल
आइए एक त्रिज्यखंड का क्षेत्रफल ज्ञात करें।
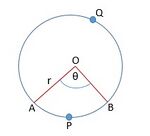
चित्र 3 में. चलो मान लें कि एक वृत्त का त्रिज्यखंड है जिसका केंद्र , और त्रिज्या है तथा , 𝜃 है।
हम जानते हैं कि एक वृत्त का क्षेत्रफल है।
जब केंद्र पर कोण के माप का घात है, तो त्रिज्यखंड का क्षेत्रफल = है, इसलिए जब केंद्र पर कोण के माप का घात है,
तो त्रिज्यखंड का क्षेत्रफल =
| कोण के त्रिज्यखंड का क्षेत्रफल=,जहाँ वृत्त की त्रिज्या है और घात में त्रिज्यखंड का कोण है। |
|---|
त्रिज्यखंड संगत चाप की लम्बाई एवं क्षेत्रफल
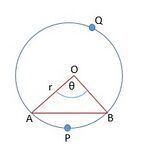
चित्र 4 में।
जब केंद्र पर कोण की माप का घात है, तो चाप की लंबाई =
अत: जब केंद्र पर कोण की माप का घात है, तो चाप की लंबाई = होती है
| चाप की लंबाई = |
|---|
वृत्तखंड का क्षेत्रफल = त्रिज्यखण्ड का क्षेत्रफल - का क्षेत्रफल
चित्र 3 और चित्र 4 से
दीर्घ त्रिज्यखंड का क्षेत्रफल = – लघु त्रिज्यखंड का क्षेत्रफल
दीर्घ वृत्तखंड का क्षेत्रफल = – लघु वृत्तखंड का क्षेत्रफल
उदाहरण
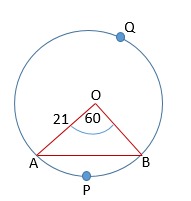
cm त्रिज्या वाले एक वृत्त में, एक चाप केंद्र पर का कोण अंतरित करता है।
ज्ञात करें:
(i) चाप की लंबाई (ii) चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल (iii) संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल
यहाँ
(i) चाप की लंबाई =
= = = cm
(ii) त्रिज्यखंड का क्षेत्रफल =
= = = cm2
(iii)वृत्तखंड का क्षेत्रफल संगत जीवा द्वारा निर्मित = त्रिज्यखंड का क्षेत्रफल - त्रिभुज का क्षेत्रफल
=
=
= cm2