शंकु के परिच्छेद: Difference between revisions
(image added) |
(added content) |
||
| Line 21: | Line 21: | ||
{| class="wikitable" | {| class="wikitable" | ||
|Circle | |Circle | ||
|Center is (a,b) | |Center is (a,b) | ||
Radius is r | Radius is r | ||
|<math>(x-a)^2+(y-b)^2=r^2</math> | |||
|- | |- | ||
|Ellipse with the horizontal major axis | |Ellipse with the horizontal major axis | ||
|Center is (a, b) | |Center is (a, b) | ||
Length of the major axis is 2h. | Length of the major axis is 2h. | ||
| Line 32: | Line 31: | ||
Distance between the centre and either focus is c with | Distance between the centre and either focus is c with | ||
c2=h2−k2, h>k>0 | c2=h2−k2, h>k>0 | ||
|<math>\frac{(x-a)^2}{h^2}+\frac{(y-b)^2}{k^2} =1</math> | |||
|- | |- | ||
|Ellipse with the vertical major axis | |Ellipse with the vertical major axis | ||
|Center is (a, b) | |Center is (a, b) | ||
Length of the major axis is 2h. | Length of the major axis is 2h. | ||
| Line 40: | Line 39: | ||
Distance between the centre and either focus is c with | Distance between the centre and either focus is c with | ||
c2=h2−k2, h>k>0 | c2=h2−k2, h>k>0 | ||
|<math>\frac{(x-a)^2}{k^2}+\frac{(y-b)^2}{h^2} =1</math> | |||
|- | |- | ||
|Hyperbola with the horizontal transverse axis | |Hyperbola with the horizontal transverse axis | ||
|Center is (a,b) | |Center is (a,b) | ||
Distance between the vertices is 2h | Distance between the vertices is 2h | ||
Distance between the foci is 2k. | Distance between the foci is 2k. | ||
c2=h2 + k2 | c2=h2 + k2 | ||
|<math>\frac{(x-a)^2}{h^2}-\frac{(y-b)^2}{k^2} =1</math> | |||
|- | |- | ||
|Hyperbola with the vertical transverse axis | |Hyperbola with the vertical transverse axis | ||
|Center is (a,b) | |Center is (a,b) | ||
Distance between the vertices is 2h | Distance between the vertices is 2h | ||
Distance between the foci is 2k. | Distance between the foci is 2k. | ||
c2= h2 + k2 | c2= h2 + k2 | ||
|<math>\frac{(x-a)^2}{k^2}-\frac{(y-b)^2}{h^2} =1</math> | |||
|- | |- | ||
|Parabola with the horizontal axis | |Parabola with the horizontal axis | ||
|Vertex is (a,b) | |Vertex is (a,b) | ||
Focus is (a+p,b) | Focus is (a+p,b) | ||
| Line 62: | Line 61: | ||
x=a−p | x=a−p | ||
Axis is the line y=b | Axis is the line y=b | ||
|<math>(y-b)^2=4p(x-a), p\neq0</math> | |||
|- | |- | ||
|Parabola with vertical axis | |Parabola with vertical axis | ||
|Vertex is (a,b) | |Vertex is (a,b) | ||
Focus is (a+p,b) | Focus is (a+p,b) | ||
| Line 70: | Line 69: | ||
x=b−p | x=b−p | ||
Axis is the line x=a | Axis is the line x=a | ||
|<math>(x-a)^2=4p(y-b), p\neq0</math> | |||
|} | |} | ||
| Line 75: | Line 75: | ||
इन तीन मापदंडों के अलावा, शंकु खंडों में कुछ और पैरामीटर होते हैं जैसे कि मुख्य अक्ष, लेटस रेक्टम, प्रमुख और लघु अक्ष, फोकल पैरामीटर, आदि। आइए शंकु खंड से संबंधित इन मापदंडों में से प्रत्येक के बारे में संक्षेप में जानें। शंकु खंड के मापदंडों का विवरण निम्नलिखित है। | इन तीन मापदंडों के अलावा, शंकु खंडों में कुछ और पैरामीटर होते हैं जैसे कि मुख्य अक्ष, लेटस रेक्टम, प्रमुख और लघु अक्ष, फोकल पैरामीटर, आदि। आइए शंकु खंड से संबंधित इन मापदंडों में से प्रत्येक के बारे में संक्षेप में जानें। शंकु खंड के मापदंडों का विवरण निम्नलिखित है। | ||
मुख्य अक्ष: शंकु के केंद्र और नाभियों से गुजरने वाली अक्ष इसकी मुख्य अक्ष होती है और इसे शंकु की दीर्घ अक्ष भी कहा जाता है। | * '''मुख्य अक्ष''': शंकु के केंद्र और नाभियों से गुजरने वाली अक्ष इसकी मुख्य अक्ष होती है और इसे शंकु की दीर्घ अक्ष भी कहा जाता है। | ||
* '''संयुग्म अक्ष''': मुख्य अक्ष के लंबवत खींची गई अक्ष और शंकु के केंद्र से गुजरने वाली अक्ष संयुग्म अक्ष होती है। संयुग्म अक्ष इसकी लघु अक्ष भी होती है। | |||
* '''केंद्र''': शंकु की मुख्य अक्ष और संयुग्म अक्ष के प्रतिच्छेद बिंदु को शंकु का केंद्र कहा जाता है। | |||
* '''शीर्ष''': अक्ष पर वह बिंदु जहाँ शंकु अक्ष को काटता है, शंकु का शीर्ष कहलाता है। | |||
* '''फोकल कॉर्ड''': शंकु की फोकल कॉर्ड शंकु खंड के फोकस से गुजरने वाली कॉर्ड होती है। फोकल कॉर्ड शंकु खंड को दो अलग-अलग बिंदुओं पर काटती है। | |||
* '''फोकल दूरी''': शंकु पर किसी बिंदु (x1,y1) की किसी भी नाभियों से दूरी, फोकल दूरी होती है। दीर्घवृत्त, हाइपरबोला के लिए हमारे पास दो फ़ोकस होते हैं, और इसलिए हमारे पास दो फ़ोकल दूरियाँ होती हैं। | |||
* '''लेटस रेक्टम''': यह एक फ़ोकल कॉर्ड है जो शंकु की धुरी के लंबवत होती है। परवलय के लिए लेटस रेक्टम की लंबाई LL' = 4a है। और दीर्घवृत्त और हाइपरबोला के लिए लेटस रेक्टम की लंबाई 2b2/a है। | |||
* '''स्पर्शरेखा''': स्पर्शरेखा एक रेखा है जो शंकु पर एक बिंदु पर बाहरी रूप से शंकु को छूती है। वह बिंदु जहाँ स्पर्शरेखा शंकु को छूती है उसे संपर्क बिंदु कहा जाता है। साथ ही बाहरी बिंदु से, शंकु पर लगभग दो स्पर्शरेखाएँ खींची जा सकती हैं। | |||
* '''सामान्य''': स्पर्शरेखा के लंबवत खींची गई रेखा और संपर्क बिंदु और शंकु के फ़ोकस से गुज़रने वाली रेखा को सामान्य कहा जाता है। हम शंकु पर प्रत्येक स्पर्शरेखा के लिए एक सामान्य रख सकते हैं। | |||
* '''संपर्क जीवा''': बाहरी बिंदु से शंकु तक खींची गई स्पर्श रेखाओं के संपर्क बिंदु को जोड़ने के लिए जीवा खींची जाती है, जिसे संपर्क जीवा कहते हैं। | |||
* '''ध्रुवीय और ध्रुवीय''': एक बिंदु के लिए जिसे ध्रुव कहा जाता है और शंकु खंड के बाहर स्थित होता है, इस बिंदु से खींची गई जीवाओं के सिरों पर खींची गई स्पर्श रेखाओं के प्रतिच्छेद बिंदुओं के बिन्दुपथ को ध्रुवीय कहते हैं। | |||
* '''सहायक वृत्त''': दीर्घवृत्त के प्रमुख अक्ष पर एक वृत्त खींचा जाता है क्योंकि इसका व्यास सहायक वृत्त कहलाता है। दीर्घवृत्त का शंकु समीकरण x2/a2 + y2/b2 = 1 है, और सहायक वृत्त का समीकरण x2 + y2 = a2 है। | |||
* '''निर्देशक वृत्त''': दीर्घवृत्त पर खींची गई लंबवत स्पर्श रेखाओं के प्रतिच्छेद बिंदु के बिन्दुपथ को निदेशक वृत्त कहते हैं। एक दीर्घवृत्त (x2/a2 + y2/b2 = 1) के लिए, निर्देशक वृत्त का समीकरण x2 + y2 = a2 + b2 है | |||
* '''अस्पर्शी''': हाइपरबोला के समानांतर खींची गई सीधी रेखाओं की जोड़ी और माना जाता है कि वे अनंत पर हाइपरबोला को छूती हैं। हाइपरबोला के अस्पर्शी के समीकरण क्रमशः y = bx/a, और y = -bx/a हैं। और एक हाइपरबोला के लिए जिसका शंकु समीकरण x2/a2 - y2/b2 = 1 है, हाइपरबोला के अस्पर्शी के जोड़े का समीकरण xa±yb=0है। | |||
[[Category:शंकु परिच्छेद]][[Category:कक्षा-11]][[Category:गणित]] | [[Category:शंकु परिच्छेद]][[Category:कक्षा-11]][[Category:गणित]] | ||
Revision as of 18:45, 21 November 2024
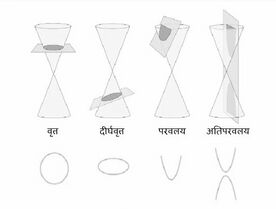
शंकु खंड या शंकु के परिच्छेद, एक समतल और शंकु के प्रतिच्छेदन द्वारा प्राप्त वक्र हैं। शंकु या शंकु के परिच्छेद के तीन प्रमुख परिच्छेद हैं: परवलय, अतिपरवलय और दीर्घवृत्त (वृत्त एक विशेष प्रकार का दीर्घवृत्त है)। शंकु के परिच्छेद का निर्माण करने के लिए दो समान आवरण वाले शंकु का उपयोग किया जाता है।
शंकु या शंकु के परिच्छेद के सभी परिच्छेदों के आकार अलग-अलग होते हैं, लेकिन उनमें कुछ सामान्य गुण होते हैं, जिनके बारे में हम निम्नलिखित अनुभागों में पढ़ेंगे।
परिभाषा
शंकु के परिच्छेद वे वक्र हैं जो तब प्राप्त होते हैं जब एक समतल शंकु को काटता है। एक शंकु में साधारणतः दो समान शंक्वाकार आकृतियाँ होती हैं जिन्हें नैप्स कहा जाता है। समतल और शंकु तथा उसके नैप्स के बीच कट के कोण के आधार पर हम विभिन्न आकृतियाँ प्राप्त कर सकते हैं। एक शंकु को समतल द्वारा विभिन्न कोणों पर काटने पर, हमें निम्नलिखित आकृतियाँ प्राप्त होती हैं:
- वृत्त
- परवलय
- दीर्घवृत्त
- अतिपरवलय
दीर्घवृत्त एक शंकु खंड है जो तब बनता है जब एक समतल शंकु को एक कोण पर काटता है। वृत्त एक विशेष प्रकार का दीर्घवृत्त है जहाँ काटने वाला समतल शंकु के आधार के समानांतर होता है। हाइपरबोला तब बनता है जब दिलचस्प समतल शंकु की धुरी के समानांतर होता है और दोहरे शंकु के दोनों नैप्स को काटता है। जब प्रतिच्छेद करने वाला समतल शंकु की सतह को एक कोण पर काटता है, तो हमें परवलय नामक एक शंकु खंड मिलता है।
शंकु के परिच्छेद मापदंड(पैरामीटर)
फोकस, डायरेक्ट्रिक्स और उत्केन्द्रता तीन महत्वपूर्ण विशेषताएं या पैरामीटर हैं जो शंकु को परिभाषित करते हैं। विभिन्न शंकु आकृतियाँ वृत्त, दीर्घवृत्त, परवलय और अतिपरवलय हैं। इन आकृतियों का आकार और अभिविन्यास पूरी तरह से इन तीन महत्वपूर्ण विशेषताओं पर आधारित है। आइए उनमें से प्रत्येक के बारे में विस्तार से जानें।
शंकु के परिच्छेद सूत्र
यहाँ दी गई तालिका में शंकु के विभिन्न प्रकार के अनुभागों के लिए सूत्र देखें।
| Circle | Center is (a,b)
Radius is r |
|
| Ellipse with the horizontal major axis | Center is (a, b)
Length of the major axis is 2h. Length of the minor axis is 2k. Distance between the centre and either focus is c with c2=h2−k2, h>k>0 |
|
| Ellipse with the vertical major axis | Center is (a, b)
Length of the major axis is 2h. Length of the minor axis is 2k. Distance between the centre and either focus is c with c2=h2−k2, h>k>0 |
|
| Hyperbola with the horizontal transverse axis | Center is (a,b)
Distance between the vertices is 2h Distance between the foci is 2k. c2=h2 + k2 |
|
| Hyperbola with the vertical transverse axis | Center is (a,b)
Distance between the vertices is 2h Distance between the foci is 2k. c2= h2 + k2 |
|
| Parabola with the horizontal axis | Vertex is (a,b)
Focus is (a+p,b) Directrix is the line x=a−p Axis is the line y=b |
|
| Parabola with vertical axis | Vertex is (a,b)
Focus is (a+p,b) Directrix is the line x=b−p Axis is the line x=a |
शंकु के परिच्छेद से संबंधित शब्द
इन तीन मापदंडों के अलावा, शंकु खंडों में कुछ और पैरामीटर होते हैं जैसे कि मुख्य अक्ष, लेटस रेक्टम, प्रमुख और लघु अक्ष, फोकल पैरामीटर, आदि। आइए शंकु खंड से संबंधित इन मापदंडों में से प्रत्येक के बारे में संक्षेप में जानें। शंकु खंड के मापदंडों का विवरण निम्नलिखित है।
- मुख्य अक्ष: शंकु के केंद्र और नाभियों से गुजरने वाली अक्ष इसकी मुख्य अक्ष होती है और इसे शंकु की दीर्घ अक्ष भी कहा जाता है।
- संयुग्म अक्ष: मुख्य अक्ष के लंबवत खींची गई अक्ष और शंकु के केंद्र से गुजरने वाली अक्ष संयुग्म अक्ष होती है। संयुग्म अक्ष इसकी लघु अक्ष भी होती है।
- केंद्र: शंकु की मुख्य अक्ष और संयुग्म अक्ष के प्रतिच्छेद बिंदु को शंकु का केंद्र कहा जाता है।
- शीर्ष: अक्ष पर वह बिंदु जहाँ शंकु अक्ष को काटता है, शंकु का शीर्ष कहलाता है।
- फोकल कॉर्ड: शंकु की फोकल कॉर्ड शंकु खंड के फोकस से गुजरने वाली कॉर्ड होती है। फोकल कॉर्ड शंकु खंड को दो अलग-अलग बिंदुओं पर काटती है।
- फोकल दूरी: शंकु पर किसी बिंदु (x1,y1) की किसी भी नाभियों से दूरी, फोकल दूरी होती है। दीर्घवृत्त, हाइपरबोला के लिए हमारे पास दो फ़ोकस होते हैं, और इसलिए हमारे पास दो फ़ोकल दूरियाँ होती हैं।
- लेटस रेक्टम: यह एक फ़ोकल कॉर्ड है जो शंकु की धुरी के लंबवत होती है। परवलय के लिए लेटस रेक्टम की लंबाई LL' = 4a है। और दीर्घवृत्त और हाइपरबोला के लिए लेटस रेक्टम की लंबाई 2b2/a है।
- स्पर्शरेखा: स्पर्शरेखा एक रेखा है जो शंकु पर एक बिंदु पर बाहरी रूप से शंकु को छूती है। वह बिंदु जहाँ स्पर्शरेखा शंकु को छूती है उसे संपर्क बिंदु कहा जाता है। साथ ही बाहरी बिंदु से, शंकु पर लगभग दो स्पर्शरेखाएँ खींची जा सकती हैं।
- सामान्य: स्पर्शरेखा के लंबवत खींची गई रेखा और संपर्क बिंदु और शंकु के फ़ोकस से गुज़रने वाली रेखा को सामान्य कहा जाता है। हम शंकु पर प्रत्येक स्पर्शरेखा के लिए एक सामान्य रख सकते हैं।
- संपर्क जीवा: बाहरी बिंदु से शंकु तक खींची गई स्पर्श रेखाओं के संपर्क बिंदु को जोड़ने के लिए जीवा खींची जाती है, जिसे संपर्क जीवा कहते हैं।
- ध्रुवीय और ध्रुवीय: एक बिंदु के लिए जिसे ध्रुव कहा जाता है और शंकु खंड के बाहर स्थित होता है, इस बिंदु से खींची गई जीवाओं के सिरों पर खींची गई स्पर्श रेखाओं के प्रतिच्छेद बिंदुओं के बिन्दुपथ को ध्रुवीय कहते हैं।
- सहायक वृत्त: दीर्घवृत्त के प्रमुख अक्ष पर एक वृत्त खींचा जाता है क्योंकि इसका व्यास सहायक वृत्त कहलाता है। दीर्घवृत्त का शंकु समीकरण x2/a2 + y2/b2 = 1 है, और सहायक वृत्त का समीकरण x2 + y2 = a2 है।
- निर्देशक वृत्त: दीर्घवृत्त पर खींची गई लंबवत स्पर्श रेखाओं के प्रतिच्छेद बिंदु के बिन्दुपथ को निदेशक वृत्त कहते हैं। एक दीर्घवृत्त (x2/a2 + y2/b2 = 1) के लिए, निर्देशक वृत्त का समीकरण x2 + y2 = a2 + b2 है
- अस्पर्शी: हाइपरबोला के समानांतर खींची गई सीधी रेखाओं की जोड़ी और माना जाता है कि वे अनंत पर हाइपरबोला को छूती हैं। हाइपरबोला के अस्पर्शी के समीकरण क्रमशः y = bx/a, और y = -bx/a हैं। और एक हाइपरबोला के लिए जिसका शंकु समीकरण x2/a2 - y2/b2 = 1 है, हाइपरबोला के अस्पर्शी के जोड़े का समीकरण xa±yb=0है।