नाभिलंब जीवा

गणित में, शंकु के परिच्छेद को एक वक्र के रूप में दर्शाया जाता है जो हमें शंकु की सतह के प्रतिच्छेदन से प्राप्त होता है। शंकु के परिच्छेद के विभिन्न प्रकार हैं। ये परवलय, दीर्घवृत्त और अतिपरवलय हैं। इन वक्रों को दर्शाने के लिए, कई महत्वपूर्ण शब्दों का उपयोग किया जाता है जैसे कि नाभि(फोकस), नियता(डायरेक्ट्रिक्स), नाभिलंब जीवा(लैटस रेक्टम ),बिन्दुपथ(लोकस), अनंतस्पर्शी(एसिम्टोटे), आदि। इस लेख में, हम नाभिलंब जीवा, परिभाषाएँ, नाभिलंब जीवा उदाहरण और शंकु के परिच्छेद के नाभिलंब जीवा के बारे में अध्ययन करेंगे।

शंकु के परिच्छेद के नाभिलंब जीवा को जीवा के रूप में बताया गया है जो फोकस से होकर गुजरती है और प्रमुख अक्ष के लंबवत होती है और इसमें वक्र पर दोनों अंत बिंदु उपस्थित होते हैं।

• प्रत्येक शंकु के परिच्छेद के लिए नाभिलंब जीवा की लंबाई अलग-अलग निर्दिष्ट की जाती है:
• एक वृत्त में नाभिलंब जीवा की लंबाई हमेशा एक वृत्त में व्यास की लंबाई के बराबर होती है।
• एक परवलय में नाभिलंब जीवा की लंबाई फोकल लंबाई के चार गुना के बराबर होती है।
• अतिपरवलय में नाभिलंब जीवा की लंबाई अनुप्रस्थ अक्ष की लंबाई के वर्ग के दोगुने और संयुग्मी अक्ष की लंबाई के बराबर होती है।

परिभाषा

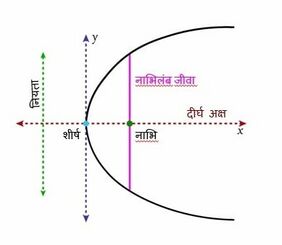
शंकु के परिच्छेद में, नाभिलंब जीवा नाभि के माध्यम से खींचा गया जीवा(कॉर्ड) है और डायरेक्ट्रिक्स के समानांतर है। लेटस शब्द लैटिन शब्द "लेटस" से लिया गया है जिसका अर्थ है पक्ष और "रेक्टम" शब्द का अर्थ है सीधा। नाभिलंब जीवा का आधा हिस्सा सेमी-नाभिलंब जीवा के रूप में जाना जाता है। नीचे दिया गया आरेख एक परवलय के नाभिलंब जीवा को दर्शाता है।

चित्र- नाभिलंब जीवा

परवलय के नाभिलंब जीवा की लंबाई

आइए हम परवलय $y^{2}=4ax$ के नाभिलंब जीवा की लंबाई को $L$और $L'$ के रूप में लें। $L$ और $L'$ के $x$ निर्देशांक “$a$” के बराबर हैं क्योंकि $S=(a,0)$

आइए हम मान लें $L=(a,b)$

जैसा कि हम जानते हैं, $L$ परवलय का बिंदु है। तदनुसार, हमारे पास है

$b^{2}=4a(a)=4a^{2}$

बाएं और दाएं दोनों तरफ वर्गमूल लेने पर, हमें $b$ बराबर $\pm 2a$ मिलता है

इसलिए, परवलय के नाभिलंब जीवा के सिरे $L=(a,2a)$ और $L'(a,-2a)$हैं

इस प्रकार, परवलय $L$ $L''$ के नाभिलंब जीवा की लंबाई $4a$ है।

अतिपरवलय के नाभिलंब जीवा की लंबाई

अतिपरवलय के नाभिलंब जीवा को दीर्घवृत्त और परवलय के स्थिति में सममित रूप से परिभाषित किया जाता है।

परवलय के नाभिलंब जीवा के अंत को $(ae,\pm {\frac {b^{2}}{a^{2}}})$ कहा जाता है और नाभिलंब जीवा की लंबाई को ${\frac {2b^{2}}{a}}$ कहा जाता है।

उदाहरण

1. नाभिलंब जीवा की लंबाई क्या होगी जिसका परवलय समीकरण $y^{2}=12x$ है

समाधान:

$y^{2}=2x$

$y^{2}=4(3)x$

चूँकि $y^{2}=4ax$ परवलय का समीकरण है, इसलिए हमें $a$ का मान प्राप्त होता है।

इसलिए, $a=3$ का मान

इस प्रकार, परवलय के नाभिलंब जीवा की लंबाई $4a=4(3)=12$ है।

2. निम्नलिखित परवलय $x^{2}=-4y$ के नाभिलंब जीवा की लंबाई क्या होगी।

समाधान: ऊपर दिए गए समीकरण से, हम यह निष्कर्ष निकाल सकते हैं कि परवलय $y$-अक्ष के बारे में सममित है और यह नीचे की ओर खुला है।

$x^{2}=-4y$

$x^{2}=-4ay$

$4a=4$

इस प्रकार, दिए गए परवलय के नाभिलंब जीवा की लंबाई $4$ इकाई है।

3. निम्नलिखित परवलय $x^{2}-2x+8y+17=0$ के नाभिलंब जीवा की लंबाई की गणना करें।

समाधान: $a$ का मान निकालने के लिए, हम पहले उपरोक्त समीकरण को मानक रूप में बदलेंगे।

$x^{2}-2x=-8y-17=0$

$x^{2}-2x(1)+1^{2}-1^{2}=-8y-17$

$(x-1)^{2}=-8y-17+1$

$(x-1)^{2}=-8y-16$

$(x-1)^{2}=-8(y+2)$

इस समीकरण से, हम यह निष्कर्ष निकाल सकते हैं कि दिया गया परवलय $y$-अक्ष के बारे में सममित है और यह ऊपर की ओर खुला है।

नाभिलंब जीवा की लंबाई $=4a$

$4a=8$

इस प्रकार, दिए गए परवलय के नाभिलंब जीवा की लंबाई $8$ इकाई है।