त्रिभुज के गुण

Theorem 1: Angles opposite to equal sides of an isosceles triangle are equal

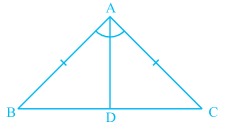
Fig 1 - Isosceles triangle

Proof: Consider an isosceles triangle $BCA$ shown in fig 1 where $AB=AC$.

We need to prove that the angles opposite to the sides $AB$ and $AC$ are equal, that is, $\angle ABC=\angle ACB$

We first draw a bisector of $\angle BAC$ and name it as $AD$.

Now in $\triangle BAD$ and $\triangle CAD$ we have,

$AB=AC$                                                       (Given)

$\angle BAD=\angle CAD$                                (By construction)

$AD=AD$                                                           (Common to both)

Thus,  $\triangle BAD\cong \triangle CAD$                            (By SAS congruence criterion)

So, $\angle ABC=\angle ACB$                                    (By CPCT)

Hence proved.

Theorem 2: The sides opposite to equal angles of a triangle are equal.

Proof: In a triangle $BCA$ shown in fig 1, base angles are equal and we need to prove that $AB=AC$ or $BCA$ is an isosceles triangle.

Construct a bisector $AD$ which meets the side $BC$ at right angles.

Now in $\triangle BAD$ and $\triangle CAD$ we have,

$\angle BAD=\angle CAD$                                        (By construction)

$AD=AD$                                                      (Common side)

$\angle BDA=\angle CDA=90^{\circ }$                                (By construction)

Thus, $\triangle BAD\cong \triangle CAD$                                   (By ASA congruence criterion)

So, $AB=AC$                                            (By CPCT)

Or $\triangle BCA$ is isosceles.