आयतचित्र
आयतचित्र, आंकडों का आलेखीय निरूपण है, जहां आंकडों को निरंतर संख्या श्रेणियों में वर्गीकृत किया जाता है तथा प्रत्येक श्रेणी एक ऊर्ध्वाधर दंड(बार) से मेल खाती है।
- क्षैतिज अक्ष संख्या परिसर प्रदर्शित करता है।
- ऊर्ध्वाधर अक्ष (बारंबारता) प्रत्येक परिसर में उपस्थित आंकडों की मात्रा को दर्शाता है।
संख्या परिसर उपयोग किए जा रहे आंकडों पर निर्भर करता है।
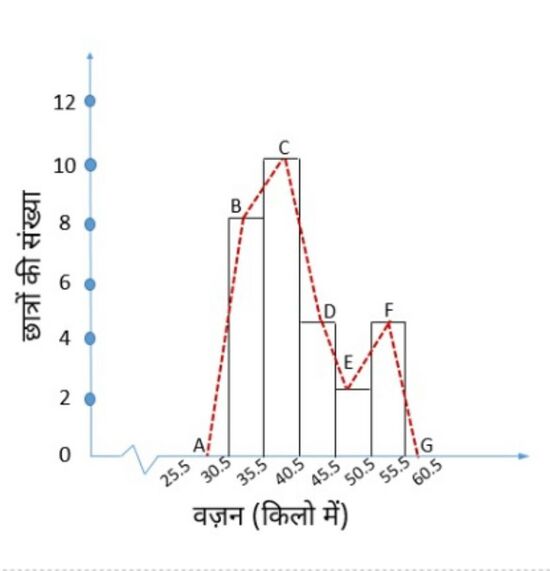
उदाहरण: निम्नलिखित बारंबारता बंटन सारणी के लिए एक आयतचित्र बनाइए जो एक कक्षा में 28 छात्रों के वज़न की बारंबारता को वर्णित करता है।
| वज़न (किलो में) | छात्रों की संख्या |
|---|---|
| 30.5 - 35.5 | 8 |
| 35.5 - 40.5 | 10 |
| 40.5 - 45.5 | 4 |
| 45.5 - 50.5 | 2 |
| 50.5 - 55.5 | 4 |
| कुल | 28 |
आइए ऊपर दिए गए आंकडों को आलेखीय रूप से इस प्रकार प्रस्तुत करें:
(i) हम क्षैतिज अक्ष पर भारों/वज़न को उपयुक्त पैमाने पर निरूपित करते हैं। हम पैमाने को 1 सेमी = 5 किग्रा के रूप में चुन सकते हैं। साथ ही, चूंकि प्रथम वर्ग अंतराल 30.5 से प्रारंभ हो रहा है, शून्य से नहीं, इसलिए हम इसे अक्ष पर एक विराम चिह्नित करके आलेख पर दिखाते हैं।
(ii) हम ऊर्ध्वाधर अक्ष पर छात्रों की संख्या (बारंबारता) को उपयुक्त पैमाने पर दर्शाते हैं। चूंकि अधिकतम बारंबारता 10 है, इसलिए हमें इस अधिकतम बारंबारता को समायोजित करने के लिए पैमाने का चयन करने की आवश्यकता है।
(iii) अब हम वर्ग आकार के समान चौड़ाई और संगत वर्ग अंतरालों की बारंबारता के अनुसार लंबाई के आयत (या आयताकार दंड/पट्टियाँ) बनाते हैं। उदाहरण के लिए, वर्ग अंतराल 30.5-35.5 के लिए आयत की चौड़ाई 1 सेमी और लंबाई 4 सेमी होगी।
(iv) इस प्रकार, हम चित्र-1 में दिखाए अनुसार आलेख प्राप्त करते हैं।
ध्यान दें कि चूँकि क्रमागत आयतों के बीच कोई अंतराल नहीं है, इसलिए परिणामी आलेख एक ठोस आकृति की तरह दिखाई देता है। इसे आयतचित्र(हिस्टोग्राम) कहा जाता है, जो निरंतर वर्गों के साथ समूहीकृत बारंबारता वितरण का एक आलेखीय निरूपण है। साथ ही, दंड आलेख के विपरीत, दंड(बार) की चौड़ाई इसके निर्माण में महत्वपूर्ण भूमिका निभाती है। यहाँ, वास्तव में, खड़ी की गई आयतों के क्षेत्र संगत बारंबारता के समानुपाती हैं। हालाँकि, चूँकि आयतों की सभी चौड़ाई समान हैं, इसलिए आयतों की लंबाई बारंबारता के समानुपाती है। इसीलिए, हम उपरोक्त (iii) के अनुसार लंबाई खींचते हैं।