निर्देशांक ज्यामिति में दूरी सूत्र का उपयोग  समतल में दो बिंदुओं के बीच की दूरी ज्ञात करने के लिए किया जाता है।
समतल में दो बिंदुओं के बीच की दूरी ज्ञात करने के लिए किया जाता है।  अक्ष से किसी बिंदु की दूरी को उसका
अक्ष से किसी बिंदु की दूरी को उसका  निर्देशांक या भुज कहते हैं।
निर्देशांक या भुज कहते हैं।  अक्ष से किसी बिंदु की दूरी को उसका
अक्ष से किसी बिंदु की दूरी को उसका  निर्देशांक या कोटि कहते हैं।
निर्देशांक या कोटि कहते हैं।  अक्ष पर किसी बिंदु के निर्देशांक
अक्ष पर किसी बिंदु के निर्देशांक  के रूप के होते हैं, और
के रूप के होते हैं, और  अक्ष पर किसी बिंदु के निर्देशांक
अक्ष पर किसी बिंदु के निर्देशांक  के रूप के होते हैं। किसी समतल में किसी भी दो बिंदुओं के बीच की दूरी ज्ञात करने के लिए, हम पाइथागोरस प्रमेय का उपयोग करेंगे।
के रूप के होते हैं। किसी समतल में किसी भी दो बिंदुओं के बीच की दूरी ज्ञात करने के लिए, हम पाइथागोरस प्रमेय का उपयोग करेंगे।
दूरी-सूत्र क्या है?
दूरी सूत्र वह सूत्र है, जिसका उपयोग किसी भी दो बिंदुओं के बीच की दूरी ज्ञात करने के लिए किया जाता है, केवल तभी जब निर्देशांक हमें ज्ञात हों। ये निर्देशांक  अक्ष या
अक्ष या  अक्ष या दोनों पर स्थित हो सकते हैं। मान लीजिए, एक
अक्ष या दोनों पर स्थित हो सकते हैं। मान लीजिए, एक  समतल में दो बिंदु, मान लीजिए
समतल में दो बिंदु, मान लीजिए  और
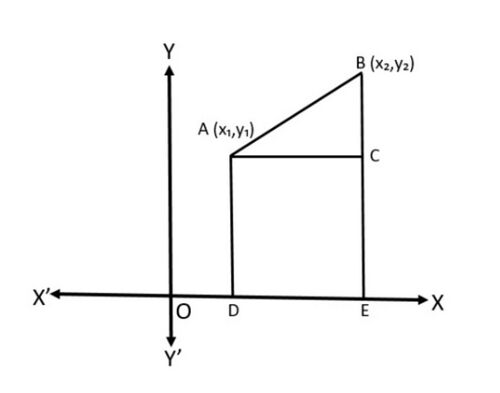
और  हैं (चित्र-1 देखें) बिंदु
हैं (चित्र-1 देखें) बिंदु  के निर्देशांक
के निर्देशांक  हैं और
हैं और  के
के  हैं।
हैं।
फिर दो बिंदुओं के बीच की दूरी ज्ञात करने का सूत्र  द्वारा दिया गया है
द्वारा दिया गया है

दूरी-सूत्र व्युत्पत्ति
आइए चित्र-1 में दर्शाए गए दो बिंदुओं  और
और  के बीच की दूरी ज्ञात करें
के बीच की दूरी ज्ञात करें
 अक्ष पर लंबवत
अक्ष पर लंबवत  और
और  खींचिए।
खींचिए।  पर बिंदु
पर बिंदु  से एक लंबवत बिंदु
से एक लंबवत बिंदु  पर मिलने के लिए खींचा जाता है।
पर मिलने के लिए खींचा जाता है।
तो,  ,
,  तो
तो  । साथ ही C
। साथ ही C ,
,  . इसलिए
. इसलिए 
अब, पाइथागोरस प्रमेय को  में लागू करते हुए , हम पाते हैं
में लागू करते हुए , हम पाते हैं


 दूरी-सूत्र है।
दूरी-सूत्र है।
उदाहरण
दोनों बिंदुओं  और
और  के बीच की दूरी ज्ञात कीजिए
के बीच की दूरी ज्ञात कीजिए
हल:
मान लीजिए 

दो बिंदुओं  और
और  के बीच की दूरी
के बीच की दूरी