रेखा की ढाल
किसी रेखा का ढलान, रेखा की ढाल और दिशा का माप है। निर्देशांक तल में रेखाओं की ढाल ज्ञात करने से यह अनुमान लगाने में सहायता मिल सकती है कि रेखाएँ समानांतर हैं, लंबवत हैं या नहीं, बिना किसी कम्पास का उपयोग किए।
किसी भी रेखा की ढाल, रेखा पर स्थित किसी भी दो अलग-अलग बिंदुओं का उपयोग करके गणना की जा सकती है। रेखा की ढाल सूत्र एक रेखा पर दो अलग-अलग बिंदुओं के बीच "ऊर्ध्वाधर परिवर्तन" और "क्षैतिज परिवर्तन" के अनुपात की गणना करता है। इस लेख में, हम ढाल ज्ञात करने की विधि और उसके अनुप्रयोगों को समझेंगे।
परिभाषा
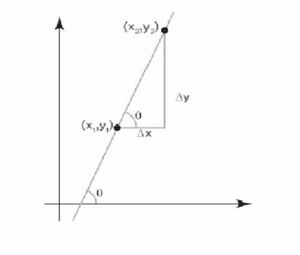
किसी रेखा की ढाल को उस रेखा के - निर्देशांक में परिवर्तन के संबंध में - निर्देशांक में परिवर्तन के रूप में परिभाषित किया जाता है। - निर्देशांक में शुद्ध परिवर्तन है, जबकि - निर्देशांक में शुद्ध परिवर्तन है। इसलिए - निर्देशांक में परिवर्तन के संबंध में - निर्देशांक में परिवर्तन को इस प्रकार लिखा जा सकता है,
जहाँ, ढलान है
ध्यान दें कि
हम इस को रेखा का ढलान भी मानते हैं।
रेखा की ढाल
रेखा की ढाल रन के लिए वृद्धि का अनुपात है, या रन द्वारा विभाजित वृद्धि है। यह निर्देशांक तल में रेखा की ढाल का वर्णन करता है। किसी रेखा के ढलान की गणना करना दो अलग-अलग बिंदुओं के बीच ढलान का पता लगाने के समान है। सामान्य तौर पर, किसी रेखा की ढाल ज्ञात करने के लिए, हमें रेखा पर किसी भी दो अलग-अलग निर्देशांक के मान की आवश्यकता होती है।
दो बिंदुओं के बीच ढलान
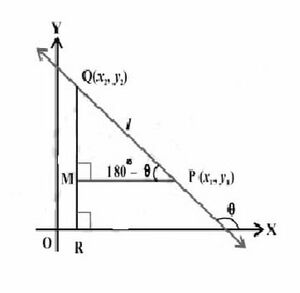
एक रेखा की ढाल की गणना एक सीधी रेखा पर स्थित दो बिंदुओं का उपयोग करके की जा सकती है। दो बिंदुओं के निर्देशांक दिए जाने पर, हम रेखा की ढाल के सूत्र को लागू कर सकते हैं। मान लें कि उन दो बिंदुओं के निर्देशांक हैं,
जैसा कि हमने पिछले अनुभागों में चर्चा की थी, ढलान "उस रेखा के - निर्देशांक में परिवर्तन के संबंध में - निर्देशांक में परिवर्तन" है। इसलिए, ढलान के समीकरण में और के मान रखने पर, हम जानते हैं कि:
इसलिए, इन मानों का अनुपात में उपयोग करने पर, हमें यह मिलता है:
ढाल
जहाँ ढलान है, और रेखा द्वारा धनात्मक -अक्ष के साथ बनाया गया कोण है।
रेखा की ढाल सूत्र
रेखा के समीकरण से रेखा की ढाल निकाली जा सकती है। रेखा की ढाल का सामान्य सूत्र इस प्रकार दिया गया है,
जहाँ,
- ढाल है, जैसे कि
- रेखा द्वारा धनात्मक -अक्ष से बनाया गया कोण है
- , -अक्ष में शुद्ध परिवर्तन है
- , -अक्ष में शुद्ध परिवर्तन है
उदाहरण
आइए एक रेखा की ढाल की परिभाषा को याद करें और नीचे दिए गए उदाहरण को हल करने का प्रयास करें।
उदाहरण: उस रेखा का समीकरण क्या है जिसका ढलान है, और जो बिंदु से होकर गुजरती है?
समाधान:
हम जानते हैं कि यदि ढलान के रूप में दी गई है, तो सामान्य समीकरण में का मान होगा। इसलिए, हम के मान को के रूप में प्रतिस्थापित करते हैं, और हमें मिलता है,
अब, हमारे पास पहले से ही रेखा पर एक बिंदु का मान है। इसलिए, हम समीकरण में बिंदु का मान डालते हैं, और हमें मिलता है,
इसलिए, सामान्य समीकरण में और के मानों को प्रतिस्थापित करते हुए, हमें अपना अंतिम समीकरण के रूप में मिलता है।
समीकरण है:
रेखा की ढाल ज्ञात करने की विधि
हम अलग-अलग तरीकों का उपयोग करके रेखा का ढलान पता कर सकते हैं। ढलान का मान पता करने की पहली विधि इस समीकरण का उपयोग करके है,
जहाँ, रेखा का ढलान है।
साथ ही, में परिवर्तन रन है और में परिवर्तन वृद्धि या गिरावट है। इस प्रकार, हम ढलान को इस प्रकार भी परिभाषित कर सकते हैं, वृद्धि/रन
महत्वपूर्ण टिप्पणियाँ
- किसी रेखा की ढाल, -अक्ष के साथ रेखा द्वारा बनाए गए कोण के स्पर्शज्या का माप है।
- ढलान एक सीधी रेखा में स्थिर रहता है।
- सीधी रेखा की ढाल-अवरोधन रूप द्वारा दिया जा सकता है
- ढाल को अक्षर द्वारा दर्शाया जाता है, और इसे इस प्रकार दिया जाता है,