ऊँचाइयाँ और दूरियाँ
ऊँचाई और दूरियाँ का विषय त्रिकोणमिति के अनुप्रयोगों में से एक है, जिसका वास्तविक जीवन में व्यापक रूप से उपयोग किया जाता है। त्रिकोणमिति में ऊँचाई और दूरियाँ शब्दों का प्रायः उपयोग किया जाता है, जबकि इसके अनुप्रयोगों से आचरण किया जाता है। त्रिकोणमिति के ऊँचाई और दूरी के अनुप्रयोग में, निम्नलिखित अवधारणाएँ उपस्थित हैं:
- मीनारों(टावरों) की ऊँचाई मापना
- समुद्र से तट की दूरी निर्धारित करना
- दो खगोलीय पिंडों के बीच की दूरी ज्ञात करना
दृष्टि-रेखा
पर्यवेक्षक की आंखों से वस्तु पर देखे जा रहे बिंदु तक खींची गई रेखा को दृष्टि-रेखा के रूप में जाना जाता है।
उन्नयन कोण
पर्यवेक्षक द्वारा देखी गई वस्तु (क्षैतिज स्तर से ऊपर) पर बिंदु का उन्नयन कोण वह कोण है जो क्षैतिज स्तर के साथ दृष्टि-रेखा द्वारा बनता है।
अवनमन कोण
पर्यवेक्षक द्वारा देखी गई वस्तु पर स्थित बिंदु (क्षैतिज स्तर से नीचे) का अवनमन कोण, दृष्टि-रेखा और क्षैतिज स्तर के बीच बनने वाला कोण होता है।
ऊँचाई और दूरियाँ कैसे ज्ञात करें
त्रिकोणमितीय अनुपात की सहायता से किसी वस्तु की ऊँचाई या लॅंबाई या दो दूर की वस्तुओं के बीच की दूरी निर्धारित की जा सकती है।
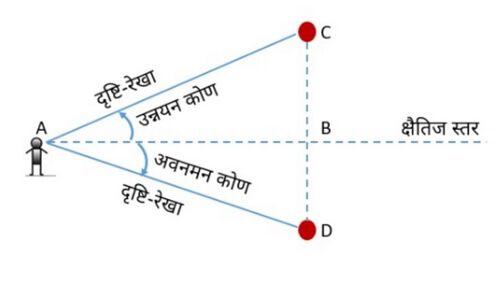
उदाहरण के लिए, चित्र-1 में, एक व्यक्ति वस्तु के शीर्ष की ओर देख रहा है। क्षैतिज स्तर है। यह स्तर पर्यवेक्षक की आंखों से गुजरने वाली जमीन के समानांतर रेखा है। को दृष्टि-रेखा के रूप में जाना जाता है। को उन्नयन कोण कहा जाता है। इसी प्रकार, चित्र-1 में, एक व्यक्ति नीचे किसी वस्तु को देख रहा है। क्षैतिज स्तर है। यह स्तर पर्यवेक्षक की आंखों से गुजरने वाली जमीन के समानांतर रेखा है। को दृष्टि-रेखा के रूप में जाना जाता है। को अवनमन कोण कहते हैं।
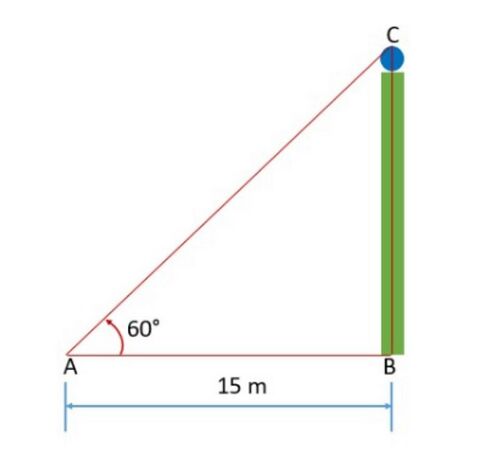
उदाहरण: एक मीनार जमीन पर लंबवत खड़ी है। जमीन पर एक बिंदु से, जो मीनार के पाद से मीटर दूर है, मीनार के शीर्ष का उन्नयन कोण है। मीनार की ऊँचाई ज्ञात कीजिए।
हल: समस्या को हल करने के लिए, हम त्रिकोणमितीय अनुपात या चुनते हैं, क्योंकि अनुपात में और उपस्थित हैं।
अतः टावर की ऊँचाई मीटर है।