Multiplication of three digit numbers by Bhārati Kṛṣṇa Tīrtha
Introduction
The general formula of multiplication which will be applicable to multiplication of 3 digit number with 3 digit or 2 digit number.
Here is the Sūtra
ऊर्ध्वतिर्यग्भ्याम्
Ūrdhvatiryagbhyām
(vertical and crosswise)
will be used.
Multiplication of a 3 digit number with 3 digit number or 2 digit number[1]
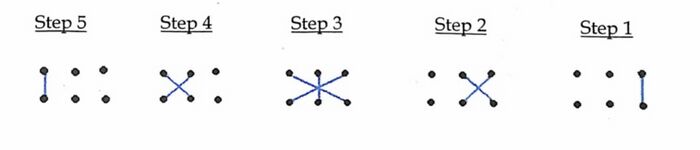
Columns are counted from the right side
Step 1 :Vertically multiply the two digits in the first column.
Step 2 : Cross multiply the first digit of the first column with the second digit of the second column. Second digit of the first column with the first digit of the second column and add the two products.
Step 3 : Cross multiply the first digit of the first column with the second digit of the third column. Second digit of the first column with the first digit of the third column. Vertically multiply the two digits in the second column and add the three products.
Step 4 : Cross multiply the first digit of the second column with the second digit of the third column. Second digit of the second column with the first digit of the third column and add the two products.
Step 5 :Vertically multiply the two digits in the third column.
Multiplication of a 3 digit number with 3 digit number
Example: 123 X 645
| Third Column | Second Column | First Column | |
|---|---|---|---|
| First Digit | 1 | 2 | 3 |
| Second Digit | 6 | 4 | 5 |
Step 1 : Vertically multiply the two digits in the first column. - 3 X 5 = 15
Step 2 : Cross multiply the first digit of the first column with the second digit of the second column. Second digit of the first column with the first digit of the second column and add the two products. - (3 X 4) + (5 X 2) = 12 + 10 = 22
Step 3 : Cross multiply the first digit of the first column with the second digit of the third column. Second digit of the first column with the first digit of the third column. Vertically multiply the two digits in the second column and add the three products. - (3 X 6) + (5 X 1) + (2 X 4) = 18 + 5 + 8 = 31
Step 4 : Cross multiply the first digit of the second column with the second digit of the third column. Second digit of the second column with the first digit of the third column and add the two products. - (2 X 6) + (4 X 1) = 12 + 4 = 16
Step 5 : Vertically multiply the two digits in the third column.- 1 X 6 = 6
Step 6 : Put the above values got from each step in the below table.
| Step 5 | Step 4 | Step 3 | Step 2 | Step 1 |
| 6 | 16 | 31 | 22 | 15 |
| 6 | 16 | 31 | 22 | Put 5 and carry over 1 |
| 6 | 16 | 31 | 22 + Carry over (1) | 5 |
| 6 | 16 | 31 | 23 | 5 |
| 6 | 16 | 31 | Put 3 and carry over 2 | 5 |
| 6 | 16 | 31 + Carry over (2) | 3 | 5 |
| 6 | 16 | 33 | 3 | 5 |
| 6 | 16 | Put 3 and carry over 3 | 3 | 5 |
| 6 | 16 + Carry over (3) | 3 | 3 | 5 |
| 6 | 19 | 3 | 3 | 5 |
| 6 | Put 9 and carry over 1 | 3 | 3 | 5 |
| 6 + carry over (1) | 9 | 3 | 3 | 5 |
| 7 | 9 | 3 | 3 | 5 |
Answer : 123 X 645 = 79335
Multiplication of a 3 digit number with 2 digit number
Example: 214 X 23
214 X 023
| Third Column | Second Column | First Column | |
|---|---|---|---|
| First Digit | 2 | 1 | 4 |
| Second Digit | 0 | 2 | 3 |
Step 1 : Vertically multiply the two digits in the first column. - 4 X 3 = 12
Step 2 : Cross multiply the first digit of the first column with the second digit of the second column. Second digit of the first column with the first digit of the second column and add the two products. - (4 X 2) + (3 X 1) = 8 + 3 = 11
Step 3 : Cross multiply the first digit of the first column with the second digit of the third column. Second digit of the first column with the first digit of the third column. Vertically multiply the two digits in the second column and add the three products. - (4 X 0) + (3 X 2) + (1 X 2) = 0 + 6 + 2 = 8
Step 4 : Cross multiply the first digit of the second column with the second digit of the third column. Second digit of the second column with the first digit of the third column and add the two products. - (1 X 0) + (2 X 2) = 0 + 4 = 4
Step 5 : Vertically multiply the two digits in the third column.- 2 X 0 = 0
Step 6 : Put the above values got from each step in the below table.
| Step 5 | Step 4 | Step 3 | Step 2 | Step 1 |
| 0 | 4 | 8 | 11 | 12 |
| 0 | 4 | 8 | 11 | Put 2 and carry over 1 |
| 0 | 4 | 8 | 11 + Carry over (1) | 2 |
| 0 | 4 | 8 | 12 | 2 |
| 0 | 4 | 8 | Put 2 and carry over 1 | 2 |
| 0 | 4 | 8 + Carry over (1) | 2 | 2 |
| 0 | 4 | 9 | 2 | 2 |
Answer : 123 X 645 = 4922
Multiplication of a 2 digit number with 3 digit number
Example: 57 X 346
057 X 346
| Third Column | Second Column | First Column | |
|---|---|---|---|
| First Digit | 0 | 5 | 7 |
| Second Digit | 3 | 4 | 6 |
Step 1 : Vertically multiply the two digits in the first column. - 7 X 6 = 42
Step 2 : Cross multiply the first digit of the first column with the second digit of the second column. Second digit of the first column with the first digit of the second column and add the two products. - (7 X 4) + (6 X 5) = 28 + 30 = 58
Step 3 : Cross multiply the first digit of the first column with the second digit of the third column. Second digit of the first column with the first digit of the third column. Vertically multiply the two digits in the second column and add the three products. - (7 X 3) + (6 X 0) + (5 X 4) = 21 + 0 + 20 = 41
Step 4 : Cross multiply the first digit of the second column with the second digit of the third column. Second digit of the second column with the first digit of the third column and add the two products. - (5 X 3) + (4 X 0) = 15 + 0 = 15
Step 5 : Vertically multiply the two digits in the third column.- 0 X 3 = 0
Step 6 : Put the above values got from each step in the below table.
| Step 5 | Step 4 | Step 3 | Step 2 | Step 1 |
| 0 | 15 | 41 | 58 | 42 |
| 0 | 15 | 41 | 58 | Put 2 and carry over 4 |
| 0 | 15 | 41 | 58 + Carry over (4) | 2 |
| 0 | 15 | 41 | 62 | 2 |
| 0 | 15 | 41 | Put 2 and carry over 6 | 2 |
| 0 | 15 | 41 + Carry over (6) | 2 | 2 |
| 0 | 15 | 47 | 2 | 2 |
| 0 | 15 | Put 7 and carry over 4 | 2 | 2 |
| 0 | 15 + Carry over (4) | 7 | 2 | 2 |
| 0 | 19 | 7 | 2 | 2 |
| 0 | Put 9 and carry over 1 | 7 | 2 | 2 |
| 0 + Carryover (1) | 9 | 7 | 2 | 2 |
| 1 | 9 | 7 | 2 | 2 |
Answer : 57 X 346 = 19722
See Also
References
- ↑ Singhal, Vandana (2007). Vedic Mathematics For All Ages - A Beginners' Guide. Delhi: Motilal Banarsidass. pp. 107–114. ISBN 978-81-208-3230-5.