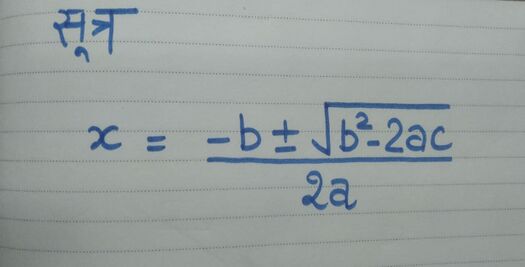श्रीधराचार्य
इस इकाई में आईए हम जानते हैं प्रख्यात गणितज्ञ श्रीधराचार्य जी के जीवन परिचय के बारे में ।
जीवन परिचय
श्रीधराचार्य एक भारतीय गणितज्ञ थे जिनका जन्म 870 ई. में हुआ था और उनकी मृत्यु सी. में हुई थी। 930 ई.पू. गणितज्ञ होने के अलावा, वह एक दार्शनिक और संस्कृत पंडित भी थे।उनका जन्म भूरिश्रेष्ठी में हुआ था जिसे वर्तमान में हुगली के नाम से जाना जाता है।
श्रीधराचार्य जी द्वारा लिखे गए प्रमुख पांच गणित के ग्रंथ हैं-
1.त्रिशतिका
2.पाटीगणित
3.बीजगणित
4.नवसती
5.बृहत्पति
उन्होंने अपनी एक पुस्तक में तीन सौ से अधिक श्लोक लिखे हैं और इसलिए वह पुस्तक त्रिशतिका के नाम से प्रसिद्ध है। अपनी पुस्तकों में, उन्होंने संख्याओं की गिनती, अंश, संयुक्त व्यवसाय या साझेदारी, विभाजन, वर्ग, घन, प्राकृतिक संख्या, शून्य, ब्याज-गणना, तीन का नियम, माप, गुणन और क्षेत्रमिति (ज्यामिति का मुख्य भाग जो आकार, लंबाई, क्षेत्रफल और आयतन से संबंधित है)।
गणित में श्रीधराचार्य का योगदान
1.उन्होंने ही बीजगणित को अंकगणित से अलग किया।
2.उन्होंने शून्य पर स्पष्टीकरण दिया, उन्होंने संबोधित करते हुए कहा, “यदि किसी संख्या में शून्य जोड़ा जाता है, तो योग वही संख्या होती है, यदि शून्य को किसी संख्या से गुणा किया जाए, तो गुणनफल शून्य होता है, यदि किसी संख्या में से शून्य घटा दिया जाए ,तो वह संख्या अपरिवर्तित रहती है।”
3.उन्होंने बीजगणित के व्यावहारिक अनुप्रयोगों पर विचार प्रस्तुत किया।
4.किसी भिन्न को विभाजित करते समय, उन्होंने भाजक के व्युत्क्रम से भिन्न को गुणा करने की विधि पर विचार प्रस्तुत किया।
5. वह पहले भारतीय गणितज्ञ थे जिन्होंने द्विघात समीकरणों को हल करने का सूत्र ज्ञात किया था।
श्रीधराचार्य सूत्र
श्रीधराचार्य सूत्र एक गणितीय सूत्र है जिसका उपयोग द्विघात समीकरणों को हल करने के लिए किया जाता है। श्रीधराचार्य सूत्र को सामान्यतः द्विघात सूत्र के नाम से भी जाना जाता है। श्रीधराचार्य ने द्विघात समीकरणों को हल करने की एक विधि दी और इसलिए इसका नाम महान गणितज्ञ के नाम पर रखा गया और इसे श्रीधराचार्य सूत्र कहा जाता है।
श्रीधराचार्य विधि का उपयोग ax2 + bx + c = 0, a ≠ 0 के रूप मे दिए गए द्विघात समीकरणों का हल निकालने के लिए किया जाता है।