समुच्चयों पर संक्रियाएँ

जब हम संख्याओं के युग्म पर जोड़ और गुणा की क्रिया करते हैं तो हमें एक और संख्या प्राप्त होती है। इसी प्रकार, जब हम दो समुच्चयों पर संचालन करते हैं, तो हमें एक और समुच्चय मिलता है। अब हम समुच्चय पर कुछ निश्चित संचालनों को परिभाषित करेंगे और उनके गुणों को समझेंगे।

अब से, हम अपने सभी समुच्चयों को किसी सार्वत्रिक समुच्चय के उपसमुच्चय के रूप में संदर्भित करेंगे।

File:Union - Sets.jpg

चित्र-1समुच्चयों का सम्मिलन

समुच्चयों का सम्मिलन

मान लीजिए कि $A$ और $B$ कोई दो समुच्चय हैं। समुच्चय के सम्मिलन का अर्थ है उभयनिष्ठ अवयवों को केवल एक बार रखते हुए $A$ और $B$ के सभी अवयवों को लेना। $\cup$ सम्मिलन को सूचित करने वाला प्रतीक है। प्रतीकात्मक रूप से, हम $A\cup B$ लिखते हैं,और इसे "$A$ यूनियन $B$" के रूप में पढ़ा जाता है।

उदाहरण 1

मान लीजिए $A=\{2,4,6,8\}$ और $B=\{6,8,10,12\}$

$A\cup B=\{2,4,6,8,10,12\}$। यहां इन दोनों समुच्चयों के उभयनिष्ठ अवयव $6,8$ हैं, जिन्हें $A\cup B$ दिखाते समय मात्र एक बार लिया जाता है।

उदाहरण 2

मान लीजिए $A=\{1,3,5,7,9,11,13\}$ और $B=\{1,5,9,13\}$

यहाँ $B$ , $A$ का एक उपसमुच्चय है। समुच्चय $A$ और उसके उपसमुच्चय $B$ का सम्मिलन समुच्चय $A$ ही है।

$A\cup B=\{1,3,5,7,9,11,13\}$

अर्थात यदि $B\subset A$ तब $A\cup B=A$

परिभाषा

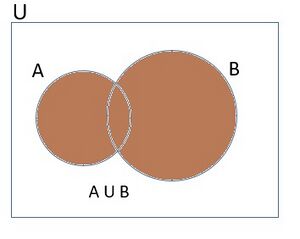
दो समुच्चय $A$ और $B$ का सम्मिलन समुच्चय $C$ है जिसमें वे सभी तत्व समिलित होते हैं जो या तो $A$ में हैं या $B$ में हैं जिनमें वे भी समिलित हैं जो दोनों में हैं)। प्रतीकों में हम https://alpha.indicwiki.in/index.php?title=Special:MathShowImage&hash=08f9fad30ed594e7591a3e04a8d7774c&mode=mathml लिखते हैं। दो समुच्चयों के सम्मिलन को वेन आरेख द्वारा दर्शाया जा सकता है, जैसा चित्र-1 में दर्शाया गया है।

चित्र-1 में छायांकित भाग $A\cup B$ को दर्शाता है।