त्रिभुज का क्षेत्रफल - हीरोन के सूत्र द्वारा
हीरोन का परिचय
हीरोन (10 ई.पू. - 75 ई.पू.) का जन्म संभवतः लगभग 10 ई.पू. में मिस्र के अलेक्जेंड्रिया में हुआ था। उन्होंने अनुप्रयुक्त गणित में कार्य किया। गणितीय और भौतिक विषयों पर उनके कार्य इतने अधिक और विविध हैं कि उन्हें इन क्षेत्रों में एक विश्वकोश लेखक माना जाता है। उनका ज्यामितीय कार्य मुख्यतः इससे संबंधित है
क्षेत्रमिति पर समस्याएं तीन पुस्तकों में लिखी गई हैं। पुस्तक-I में वर्गों, आयतों, त्रिभुजों, समलम्ब चतुर्भुजों (ट्रैपेज़िया), विभिन्न अन्य विशिष्ट चतुर्भुजों, नियमित बहुभुजों, वृत्तों, बेलनों की सतहों, शंकुओं, गोले आदि के क्षेत्रफल का वर्णन किया गया है। इस खंड में, त्रिभुज का क्षेत्रफल उसकी तीन भुजाओं के संदर्भ में हीरोन ने प्रसिद्ध सूत्र निकाला है।
त्रिभुज का क्षेत्रफल - हीरोन के सूत्र द्वारा
हम जानते हैं कि एक त्रिभुज का क्षेत्रफल, जब उसकी ऊँचाई दी जाती है, × आधार × ऊँचाई होती है। अब मान लीजिए कि हम एक विषमकोण त्रिभुज की भुजाओं की लंबाई जानते हैं, ऊंचाई नहीं। हम इसका क्षेत्रफल कैसे ज्ञात करेंगे? उदाहरण के लिए, आपके पास एक त्रिकोणीय पार्क है जिसकी भुजाएँ मी, मी, और हैं मीटर हम इसका क्षेत्रफल कैसे निकालेंगे? निःसंदेह, यदि हम सूत्र को लागू करना चाहते हैं, तो हमें इसकी ऊंचाई की गणना करनी होगी। हालाँकि, हमें यह नहीं पता कि ऊँचाई की गणना कैसे करें।
हीरोन द्वारा त्रिभुज के क्षेत्रफल के बारे में दिए गए सूत्र को हीरो का सूत्र भी कहा जाता है। इसे इस प्रकार बताया गया है:
त्रिभुज का क्षेत्रफल =
जहाँ त्रिभुज की भुजाएँ हैं, और = अर्ध-परिधि, अर्थात, त्रिभुज की आधी परिधि
उदाहरण
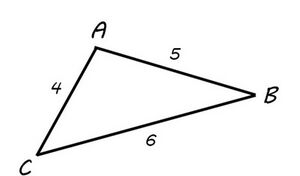
1.चित्र में दर्शाए गए त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
मान लीजिए
त्रिभुज का क्षेत्रफल=
=
=
=
= इकाइयाँ
2.एक त्रिभुजाकार भूखंड की भुजाएँ के अनुपात में हैं तथा इसका परिमाप मीटर है। इसका क्षेत्रफल ज्ञात कीजिए।
हल: मान लीजिए कि मीटर में भुजाएँ हैं
तब, हम जानते हैं कि त्रिभुज का परिमाप
अतः भुजाएँ मीटर में हैं
m
त्रिभुज का क्षेत्रफल =
=
=
= m2