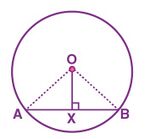
केंद्र से जीवा पर लंब
गणित में, जीवा एक रेखा खंड है जो एक वृत्त की परिधि पर दो बिंदुओं को जोड़ती है। हम जानते हैं कि किसी वृत्त की सबसे लंबी जीवा वह व्यास होती है जो वृत्त के केंद्र से होकर गुजरती है। इस लेख में वृत्त के केन्द्र से लंब से सम्बंधित प्रमेय और उसके प्रमाण तथा इस प्रमेय के व्युत्क्रम पर विस्तार से चर्चा की गई है।
केंद्र से जीवा पर लंब– प्रमेय एवं प्रमाण
प्रमेय :
एक वृत्त के केंद्र से जीवा पर डाला गया लंब, जीवा को समद्विभाजित करता है।
प्रमाण:
चित्र-1 में दिखाए गए केंद्र वाले वाले एक वृत्त पर विचार करें
एक जीवा है जिससे रेखा जीवा पर लंबवत है।
हमें प्रमाणित करने की आवश्यकता है:
दो त्रिभुजों और पर विचार करें
(समान भुजाएँ)
(त्रिज्या)
RHS नियम का उपयोग करके, हम सिद्ध कर सकते हैं कि त्रिभुज , के सर्वांगसम है।
अतः,
अत: हम ऐसा कह सकते हैं (CPCT द्वारा)
इस प्रकार, यह सिद्ध होता है कि वृत्त के केन्द्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है।
इस प्रमेय का व्युत्क्रम:
किसी जीवा को समद्विभाजित करने के लिए वृत्त के केंद्र से होकर खींची गई रेखा जीवा पर लंबवत होती है
प्रमाण:
चित्र-1 पर विचार करें
मान लीजिए केंद्र वाले वृत्त की जीवा है।
केंद्र को जीवा के मध्यबिंदु से जोड़ा गया है।
अब, हमें प्रमाणित करने की आवश्यकता है
और को मिलाने पर दो त्रिभुज और बनते हैं
यहाँ,
(त्रिज्या)
(समान भुजाएँ)
(क्योंकि , का मध्यबिंदु है)
अत: हम ऐसा कह सकते हैं .
इस प्रकार, RHS नियम का उपयोग करके, हम प्राप्त करते हैं
इससे यह सिद्ध होता है कि वृत्त के केंद्र से होकर जीवा को समद्विभाजित करने वाली रेखा जीवा पर लंबवत होती है। अत: इस प्रमेय का व्युत्क्रम सिद्ध होता है।