माध्यमान प्रमेय
माध्य मान प्रमेय कलन में एक महत्वपूर्ण प्रमेय है। माध्य मान प्रमेय का पहला रूप 14वीं शताब्दी में भारत के केरल के गणितज्ञ परमेश्वर द्वारा प्रस्तावित किया गया था। इसके अतिरिक्त , इसका एक सरल संस्करण 17वीं शताब्दी में रोले द्वारा प्रस्तावित किया गया था: रोले का प्रमेय, जो मात्र बहुपदों के लिए सिद्ध किया गया था और कलन का भाग नहीं था। अंत में, माध्य मान प्रमेय का वर्तमान संस्करण ऑगस्टिन लुइस कॉची द्वारा वर्ष 1823 में प्रस्तावित किया गया था।
परिचय
माध्य मान प्रमेय बताता है कि दो दिए गए बिंदुओं से गुजरने वाले वक्र के लिए वक्र पर एक बिंदु होता है जहाँ स्पर्शरेखा दो दिए गए बिंदुओं से गुजरने वाली छेदक रेखा के समानांतर होती है। रोले का प्रमेय इसी माध्य मान प्रमेय से लिया गया है।
परिभाषा
माध्य मान प्रमेय बताता है कि किसी भी फलन के लिए जिसका आलेख दो दिए गए बिंदुओं से होकर गुजरता है, वक्र पर कम से कम एक बिंदु होता है जहाँ स्पर्शरेखा दो दिए गए बिंदुओं से गुजरने वाली छेदिका के समानांतर होती है। माध्य मान प्रमेय को फलन के लिए कलन(कैलकुलस) में परिभाषित किया गया है, ताकि यह एक अंतराल में सांतत्य और अवकलनीय हो।
फलन अंतराल पर सांतत्य है।
फलन अंतराल पर अवकलनीय है।
में एक बिंदु उपस्थित है जैसे कि
यहाँ हमने प्रमाणित किया है कि पर स्पर्शरेखा बिंदुओं से गुजरने वाली छेदिका के समानांतर है। इस माध्य मान प्रमेय का उपयोग बंद अंतराल में किसी कथन को सिद्ध करने के लिए किया जाता है। इसके अतिरिक्त , माध्य मान प्रमेय रोले के प्रमेय से प्राप्त होता है।
माध्य मान प्रमेय प्रमाण कथन
माध्य मान प्रमेय बताता है कि यदि कोई फलन बंद अंतराल पर सांतत्य है, और खुले अंतराल पर अवकलनीय है, तो अंतराल में कम से कम एक बिंदु उपस्थित है, जैसे कि पर फलन के परिवर्तन की औसत दर है और यह पर छेदक रेखा के समानांतर है।
प्रमाण: मान लीजिए कि की छेदक रेखा है जो और से होकर गुजरती है। हम जानते हैं कि छेदक रेखा का समीकरण है।
मान लीजिए है
से
और पर सतत है और पर अवकलनीय है।
इस प्रकार रोल्स प्रमेय को लागू करने पर, में कुछ है, जिससे
में कुछ के लिए, इस प्रकार
इस प्रकार माध्य मान प्रमेय सिद्ध होता है.
टिप्पणी : यदि फलन अवकलनीय नहीं है, यहाँ तक कि खुले अंतराल में एक बिंदु पर भी, तो परिणाम मान्य नहीं हो सकता है,
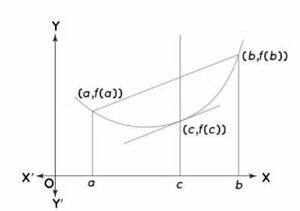
माध्य मान प्रमेय का आलेखीय निरूपण
फलन का आलेखीय निरूपण माध्य मान प्रमेय को समझने में सहायता करता है। यहाँ हम दो अलग-अलग बिंदुओं पर विचार करते हैं। इन बिंदुओं को जोड़ने वाली रेखा वक्र की छेदक रेखा है, जो वक्र को पर काटने वाली स्पर्शरेखा के समानांतर है। इन बिंदुओं को मिलाने वाले वक्र की छेदक रेखा का ढलान बिंदु पर स्पर्शरेखा के ढलान के समान है। हम जानते हैं कि स्पर्शरेखा का अवकलज उस बिंदु पर ढलान है।
स्पर्शरेखा का ढलान = छेदक रेखा का ढलान
यहाँ हम देखते हैं कि बिंदु , दो बिंदुओं के बीच स्थित है।
उदाहरण
उदाहरण : सत्यापित करें कि फलन अंतराल में माध्य मान प्रमेय को संतुष्ट करता है या नहीं। यदि हाँ, तो '' का मान ज्ञात करें।
हल: दिया गया फलन है। माध्य मान प्रमेय को सत्यापित करने के लिए, फलन को में सतत और में अवकलनीय होना चाहिए। चूँकि एक बहुपद फलन है, इसलिए उपरोक्त दोनों स्थितियाँ सत्य हैं।
अवकलज (घात नियम) अंतराल में परिभाषित किया गया है
जो कि अन्तराल में स्थित है
उत्तर: दिया गया फलन माध्य मान प्रमेय और को संतुष्ट करता है।
माध्य मान प्रमेय और रोले के प्रमेय के बीच अंतर
माध्य मान प्रमेय और रोले के प्रमेय दोनों ही फलन को इस तरह परिभाषित करते हैं कि यह अंतराल में सांतत्य है, और यह अंतराल में अवकलनीय है। माध्य मान प्रमेय में, दो संदर्भित बिंदु अलग-अलग हैं और है। रोले के प्रमेय में, बिंदुओं को इस तरह परिभाषित किया जाता है कि ।
माध्य मान प्रमेय में का मान इस तरह परिभाषित किया जाता है कि बिंदु पर स्पर्शरेखा की ढलान दो बिंदुओं को जोड़ने वाली छेदक की ढलान के समान होती है। रोले के प्रमेय में का मान इस तरह परिभाषित किया जाता है कि बिंदु पर स्पर्शरेखा की ढलान -अक्ष की ढलान के समान होती है। माध्य मान प्रमेय में ढलान है, और रोले प्रमेय में ढलान के समान है।