उच्चतम और निम्नतम

उच्चतम और निम्नतम को फलन के चरम के रूप में जाना जाता है। उच्चतम और निम्नतम किसी फलन के दिए गए परिसर के समुच्चय के भीतर अधिकतम या न्यूनतम मान हैं। फलन के लिए, संनिरपेक्ष परिसर के अंतर्गत, फलन के अधिकतम मान को निरपेक्ष उच्चतम के रूप में जाना जाता है और न्यूनतम मान को निरपेक्ष निम्नतम के रूप में जाना जाता है।

फलन के अन्य उच्चतम और निम्नतम होते हैं, जो फलन के निरपेक्ष उच्चतम और निम्नतम नहीं होते हैं और उन्हें स्थानीय उच्चतम और स्थानीय निम्नतम के रूप में जाना जाता है। आइए स्थानीय उच्चतम और निम्नतम , निरपेक्ष उच्चतम और निम्नतम के बारे में और जानें और फलन के उच्चतम और निम्नतम को कैसे खोजें।

परिभाषा

उच्चतम और निम्नतम

उच्चतम और निम्नतम किसी फलन के वक्र में चोटियाँ और घाटियाँ हैं। किसी फलन के लिए उच्चतम और निम्नतम की कोई भी संख्या हो सकती है। कैलकुलस में, हम फलन के ग्राफ़ को देखे बिना भी किसी फलन का अधिकतम और न्यूनतम मान पा सकते हैं। उच्चतम दी गई सीमा के भीतर वक्र पर सबसे ऊँचा बिंदु होगा और निम्नतम वक्र पर सबसे निचला बिंदु होगा।

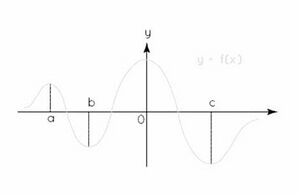
उच्चतम और निम्नतम का संयोजन चरम है। नीचे दी गई छवि में, हम ग्राफ़ में विभिन्न चोटियाँ और घाटियाँ देख सकते हैं। $x=a$ और $x=0$ पर, हमें फलन के अधिकतम मान मिलते हैं, और $x=b$ और $x=c$ पर, हमें फलन के न्यूनतम मान मिलते हैं। सभी चोटियाँ उच्चतम हैं और घाटियाँ निम्नतम हैं।

किसी फलन में दो प्रकार के उच्चतम और निम्नतम मौजूद होते हैं, जो हैं:

• स्थानीय उच्चतम और निम्नतम
• निरपेक्ष या सार्वत्रिक उच्चतम और निम्नतम

आइए इनके बारे में विस्तार से जानें।

स्थानीय अधिकतम और न्यूनतम

स्थानीय उच्चतम और निम्नतम

स्थानीय अधिकतम और न्यूनतम फलन के अधिकतम और न्यूनतम हैं जो किसी विशेष अंतराल में उत्पन्न होते हैं। स्थानीय अधिकतम एक विशेष अंतराल में एक बिंदु पर फलन का मान होगा जिसके लिए उस बिंदु के पास फलन के मान हमेशा उस बिंदु पर फलन के मान से कम होते हैं। जबकि स्थानीय न्यूनतम उस बिंदु पर फलन का मान होगा जहाँ उस बिंदु के पास फलन के मान उस बिंदु पर फलन के मान से अधिक होते हैं।

स्थानीय अधिकतम: एक बिंदु $x=b$, f(x) के लिए स्थानीय अधिकतम का एक बिंदु है यदि b के पड़ोस में है यानी (b−𝛿, b+𝛿) में जहाँ 𝛿 को मनमाने ढंग से छोटा किया जा सकता है, f(x) < f(b) सभी x ∈ (b−𝛿, b+𝛿)∖{b} के लिए। इसका सीधा सा मतलब है कि अगर हम $x=b$ के आस-पास एक छोटा क्षेत्र (अंतराल) मानते हैं, तो f(b) उस अंतराल में अधिकतम होना चाहिए।

स्थानीय न्यूनतम: एक बिंदु $x=a$, f(x) के लिए स्थानीय न्यूनतम का एक बिंदु है यदि a के पड़ोस में है, यानी (a−𝛿,a+𝛿) में, (जहाँ 𝛿 के मनमाने ढंग से छोटे मान हो सकते हैं), f(x) > f(a) सभी x ∈ (a−𝛿,a+𝛿)∖{a} के लिए। इसका अर्थ यह है कि यदि हम $x=a$ के आस-पास एक छोटा अंतराल लें, तो f(a) उस अंतराल में न्यूनतम होना चाहिए।

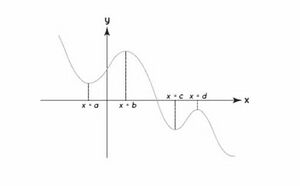
नीचे दी गई छवि में, हम देख सकते हैं कि $x=b$ और x = d, स्थानीय उच्चतम हैं, और $x=a$ और x = c, स्थानीय निम्नतम हैं।

निरपेक्ष उच्चतम और निम्नतम

निरपेक्ष उच्चतम और निम्नतम

संनिरपेक्ष प्रांत के भीतर किसी फलन का उच्चतम बिंदु फलन का निरपेक्ष उच्चतम कहलाता है जबकि फलन के संनिरपेक्ष प्रांत के भीतर फलन का निम्नतम बिंदु फलन का निरपेक्ष निम्नतम कहलाता है। संनिरपेक्ष प्रांत पर फलन का केवल एक निरपेक्ष उच्चतम और फलन का एक निरपेक्ष निम्नतम हो सकता है। फलन के निरपेक्ष उच्चतम और निम्नतम को फलन का सार्वत्रिक उच्चतम और सार्वत्रिक निम्नतम भी कहा जा सकता है।

निरपेक्ष मैक्सिमा: एक बिंदु $x=af(x)$ के लिए सार्वत्रिक उच्चतम का बिंदु है यदि सभी $x\in D,(f(x)$ का प्रांत $)$ के लिए $f(x)\leq f(a)$है।

निरपेक्ष मिनिमा: एक बिंदु $x=af(x)$ के लिए सार्वत्रिक निम्नतम का बिंदु है यदि सभी $x\in D,(f(x)$का प्रांत $)$ के लिए $f(x)\geq f(a)$ है।

नीचे दी गई छवि में, बिंदु $x=a$ फलन का निरपेक्ष उच्चतम है और $x=b$ पर फलन का निरपेक्ष निम्नतम है।

किसी फलन का उच्चतम और निम्नतम ज्ञात करने की विधि

फलन का उच्चतम और निम्नतम पहले-क्रम अवकलन परीक्षण और दूसरे-क्रम अवकलन परीक्षण का उपयोग करके गणना की जा सकती है। अवकलन परीक्षण किसी फलन का उच्चतम और निम्नतम खोजने का सबसे तेज़ तरीका है। आइए हम उन पर एक-एक करके चर्चा करें।

उच्चतम और निम्नतम के लिए प्रथम क्रम अवकलन परीक्षण

किसी फलन का पहला अवकलन फलन का ढलान देता है। अधिकतम बिंदु के पास, वक्र का ढलान बढ़ता है क्योंकि हम अधिकतम बिंदु की ओर बढ़ते हैं फिर अधिकतम बिंदु पर $0$ हो जाता है और फिर अधिकतम बिंदु से दूर जाने पर घटता है। इसी तरह, न्यूनतम बिंदु के पास, फलन का ढलान घटता है क्योंकि हम न्यूनतम बिंदु की ओर बढ़ते हैं फिर न्यूनतम बिंदु पर $0$ हो जाता है और फिर न्यूनतम बिंदु से दूर जाने पर बढ़ता है। हम इस जानकारी का उपयोग यह जानने के लिए करते हैं कि बिंदु अधिकतम है या न्यूनतम।

मान लें कि हमारे पास एक फलन $f$ है जो एक खुले अंतराल I में परिभाषित महत्वनिरपेक्ष बिंदु पर निरंतर है और $f'(c)=0$ (ढलान $c$ पर $0$ है)। फिर हम वक्र के बाईं ओर और वक्र के दाईं ओर बिंदु पर $f'(x)$ का मान जाँचते हैं और $f'(x)$ की प्रकृति की जाँच करते हैं, फिर हम कह सकते हैं कि दिया गया बिंदु होगा:

• स्थानीय उच्चतम  : यदि बिंदु $c$ से $x$ बढ़ने पर $f'(x)$ का चिह्न धनात्मक से ऋणात्मक में बदल जाता है, तो $f(c)$ उस श्रेणी में फलन का अधिकतम मान देता है।
• स्थानीय निम्नतम : यदि बिंदु $c$ से $x$ बढ़ने पर $f'(x)$ का चिह्न ऋणात्मक से धनात्मक में बदल जाता है, तो $f(c)$ उस श्रेणी में फलन का न्यूनतम मान देता है।
• परिवर्तन बिंदु: यदि $c$ से $x$ बढ़ने पर $f'(x)$ का चिह्न नहीं बदलता है, और बिंदु $c$ फलन का न तो उच्चतम है और न ही निम्नतम , तो बिंदु $c$ को विभक्ति बिंदु कहा जाता है।

उच्चतम और निम्नतम के लिए द्वितीय-क्रम अवकलन परीक्षण

उच्चतम और निम्नतम के लिए द्वितीय-क्रम अवकलन परीक्षण में, हम फलन का पहला अवकलन पाते हैं और यदि यह महत्वनिरपेक्ष बिंदु $x=c(f'(c)=0)$ पर ढलान का मान $0$ के बराबर देता है, तो हम फलन का दूसरा अवकलन पाते हैं। यदि फलन का दूसरा अवकलन दी गई सीमा के भीतर मौजूद है, तो दिया गया बिंदु होगा:

• स्थानीय अधिकतम: यदि $f''(c)<0$
• स्थानीय न्यूनतम: यदि $f''(c)>0$
• परीक्षण विफल: यदि $f''(c)=0$

उच्चतम और निम्नतम पर महत्वनिरपेक्ष नोट्स:

• उच्चतम और निम्नतम किसी फलन के वक्र में चोटियाँ और घाटियाँ हैं।
• किसी फलन का केवल एक निरपेक्ष उच्चतम और पूरे प्रांत पर फलन का एक निरपेक्ष निम्नतम हो सकता है।
• अंतराल $I$ में फलन $f$ को एक नीरस फलन कहा जाता है, यदि $f$ या तो $I$ में बढ़ रहा है या $I$ में घट रहा है।