समाकलन को अवकलन के व्युत्क्रम प्रक्रम के रूप में
समाकलन, एक संपूर्ण को ज्ञात करने के लिए भाग को एकजुट करने का एक उपाय है। समाकलन कलन में, हम एक ऐसा फलन पाते हैं जिसका अंतर दिया गया है। इस प्रकार समाकलन अवकलन का प्रतिलोम है। समाकलन का उपयोग फलन के आलेख द्वारा परिबद्ध क्षेत्र के क्षेत्र को परिभाषित करने और गणना करने के लिए किया जाता है। वक्र आकार का क्षेत्र इसमें अंकित बहुभुज की भुजाओं की संख्या को ज्ञात कर अनुमानित किया जाता है। निःशेषण(क्सहॉशन) की विधि के रूप में जानी जाने वाली इस प्रक्रिया को बाद में समाकलन के रूप में अपनाया गया।
परिचय
समाकलन को अवकलन के व्युत्क्रम प्रक्रम के रूप मेंएक विधि है, जो बड़े पैमाने पर फलनों को संक्षेप में प्रस्तुत करती है। इस लेख में, आइए कुछ विशिष्ट फलनों के समाकलन पर चर्चा करें जो साधारणतः गणना के लिए उपयोग किए जाते हैं। इन समाकलन के वास्तविक जीवन में भी कई तरह के अनुप्रयोग हैं, जैसे कि वक्रों के बीच का क्षेत्र ज्ञात करना, आयतन ज्ञात करना, किसी फलन का औसत मान ज्ञात करना, द्रव्यमान का केंद्र, गतिज ऊर्जा, किए गए कार्य की मात्रा, और बहुत कुछ।
कई महत्वपूर्ण समाकलन सूत्र हैं जो कई अन्य मानक समाकलनों को एकीकृत करने के लिए लागू किए जाते हैं। इस लेख में, हम इन विशिष्ट फलनों के समाकलनों पर एक दृष्टि डालेंगे और देखेंगे कि उनका उपयोग कई अन्य मानक समाकलनों में कैसे किया जाता है।
परिभाषा
हम समाकल के दो रूप प्राप्त करते हैं, अनिश्चित और निश्चित समाकल। अवकलन और समाकलन कलन में मौलिक उपकरण हैं जिनका उपयोग गणित और भौतिकी में समस्याओं को हल करने के लिए किया जाता है। समाकलन के सिद्धांत लाइबनिज द्वारा तैयार किए गए थे। आइए आगे बढ़ते हैं और समाकलन , इसके गुणों और इसकी कुछ शक्तिशाली तकनीकों के बारे में सीखते हैं।
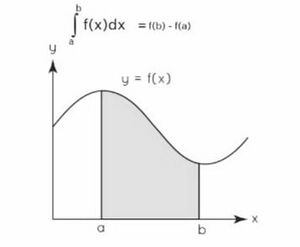
समाकलन वक्र के नीचे के क्षेत्र का क्षेत्रफल ज्ञात करने की प्रक्रिया है। यह क्षेत्र को आवरण करने वाले जितने भी छोटे आयत हों, उन्हें खींचकर और उनके क्षेत्रों को जोड़कर किया जाता है। योग एक सीमा के निकट पहुंचता है जो फलन के वक्र के नीचे के क्षेत्र के समान होता है। समाकलन फलन के प्रति अवकलज को ज्ञात करने की प्रक्रिया है। यदि कोई फलन समाकलनीय है और यदि प्रांत पर उसका समाकलन परिमित है, जिसकी सीमाएँ निर्दिष्ट हैं, तो यह निश्चित समाकलन है।
समाकलन
यदि कोई फ़ंक्शन समाकलनीय है और यदि डोमेन पर उसका समाकलन परिमित है, तथा सीमाएँ निर्दिष्ट हैं, तो वह निश्चित समाकलन है।
If d/dx(F(x) = f(x), then ∫ f(x) dx = F(x) +C. These are indefinite integrals. For example, let f(x) = x3 be a function. The derivative of f(x) is f’(x) = 3x2 and the antiderivative of 3x2 is f(x) = x3
| Function F(x) | Derivative F'(x) = f(x) | Antiderivative of f(x) |
| x3 + 0 | 3x2 | x3 + ? |
| x3 + 2 | 3x2 | x3 + ? |
| x3 - 4 | 3x2 | x3 + ? |
इस प्रकार हम पाते हैं कि F(x) के व्युत्पन्न = f(x) हैं, हालाँकि, f(x) के प्रति-व्युत्पन्न अद्वितीय नहीं हैं। f(x) का प्रति-व्युत्पन्न अनंत रूप से कई कार्यों का एक परिवार है। वास्तव में, इस फ़ंक्शन के अनंत समाकलन मौजूद हैं क्योंकि किसी भी वास्तविक स्थिरांक C का व्युत्पन्न शून्य है और हम इसे ∫ cos x. dx = sin x + C के रूप में लिख सकते हैं। वास्तविक संख्याओं के सेट से एक मनमाना स्थिरांक C जोड़ना समाकलन का नियम है। इस प्रकार हम निष्कर्ष निकालते हैं कि, यदि
dydx=f(x), तो हम लिखते हैं
y=∫f(x)dx
जिसे "x के संबंध में f का समाकलन" के रूप में पढ़ा जाता है।
प्रमेय: यदि F(x) अंतराल I पर f(x) का एक विशेष प्रतिअवकलज है, तो I पर f(x) का प्रत्येक प्रतिअवकलज ∫ f(x) dx = F(x) + C द्वारा दिया जाता है।
- यहाँ, ∫ f(x) dx समाकलन के पूरे वर्ग को दर्शाता है।
- C मनमाना स्थिरांक है, और I पर f(x) के सभी प्रतिअवकलज C को एक विशेष मान देकर प्राप्त किए जा सकते हैं।
- यहाँ f(x) समाकलन है,
- dx में चर x को समाकलक कहा जाता है और समाकलन खोजने की पूरी प्रक्रिया को समाकलन कहा जाता है। ∫ चिह्न योग को दर्शाता है।
समाकलन को अवकलन के व्युत्क्रम प्रक्रम के रूप में
हमें एक फ़ंक्शन का व्युत्पन्न दिया गया है और हमें इसका आदिम, यानी मूल फ़ंक्शन खोजने के लिए कहा गया है। ऐसी प्रक्रिया को प्रति-विभेदन या समाकलन कहा जाता है। यदि हमें किसी फ़ंक्शन का व्युत्पन्न दिया जाता है, तो मूल फ़ंक्शन को खोजने की प्रक्रिया को समाकलन कहा जाता है। व्युत्पन्न और समाकल एक दूसरे के विपरीत होते हैं। एक फ़ंक्शन f(x)= sin x पर विचार करें। f(x) का व्युत्पन्न f'(x) = cos x है। हम कहते हैं कि फ़ंक्शन cos x sin x का व्युत्पन्न फ़ंक्शन है। इसी तरह, हम कहते हैं कि sin x cos x का प्रति-व्युत्पन्न है।
समाकलन के गुण
अनिश्चित समाकल के कुछ गुण इस प्रकार हैं:
- ∫ [f(x)±g(x)] dx =∫ f(x) dx ± ∫ g(x) dx
- ∫ k f(x) dx = k ∫ f(x) dx, where k is any real number.
- ∫ f(x) dx = ∫ g(x) dx, if ∫ [f(x)-g(x)] dx = 0
- The combination of first two properties arise to∫[k1f1(x)dx+k2f2(x)dx+.........knf(x)dx]=k1∫f1(x)dx+k2∫f2(x)dx+....+kn∫f(x)dx