निश्चित समाकलन
निश्चित समाकलन आलेख में वक्र का क्षेत्रफल ज्ञात करने में सहायता करता है। इसकी सीमाएँ होती हैं: आरंभ और अंत बिंदु जिसके भीतर वक्र के नीचे का क्षेत्रफल परिकलित किया जाता है। मान लें कि -अक्ष के सापेक्ष वक्र का क्षेत्रफल ज्ञात करने के लिए सीमा बिंदु हैं। तब निश्चित समाकलन की संगत व्यंजक है। समाकलन क्षेत्रों का योग है, और सीमाओं के भीतर का क्षेत्रफल ज्ञात करने के लिए निश्चित समाकलन का उपयोग किया जाता है।
समाकलन का अध्ययन तीसरी शताब्दी ईसा पूर्व में प्रारंभ हुआ था, जिसका उपयोग वृत्तों, परवलय, दीर्घवृत्त आदि का क्षेत्रफल ज्ञात करने के लिए किया जाता था। आइए हम निश्चित समाकलनों और निश्चित समाकलनों के गुणों के बारे में अधिक जानें।
परिभाषा
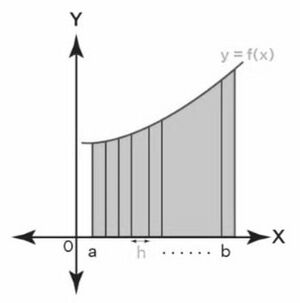
एक निश्चित समाकलन दो निश्चित सीमाओं के बीच एक वक्र के नीचे का क्षेत्र है। निश्चित समाकलन को के रूप में दर्शाया जाता है, जहाँ निचली सीमा है और ऊपरी सीमा है, -अक्ष के संदर्भ में परिभाषित फलन के लिए। दो सीमाओं के बीच एक वक्र के नीचे का क्षेत्र ज्ञात करने के लिए, हम क्षेत्र को आयतों में विभाजित करते हैं और उनका योग करते हैं। आयतों की संख्या जितनी अधिक होगी, क्षेत्र उतना ही सटीक होगा। इसलिए हम क्षेत्र को समान (बहुत छोटे) आकार वाले अनंत आयतों में विभाजित करते हैं और सभी क्षेत्रों को जोड़ते हैं। यह मूलभूत सिद्धांत है जो निश्चित समाकलन के पीछे निहित है।
निश्चित समाकलन सूत्र
निश्चित समाकलन सूत्रों का उपयोग निश्चित समाकलन का मूल्यांकन करने के लिए किया जाता है। हमारे पास नीचे बताए गए अनुसार निश्चित समाकलन का मूल्यांकन करने के लिए दो सूत्र हैं। पहले सूत्र को "सीमा योग के रूप में निश्चित समाकलन" कहा जाता है और दूसरे सूत्र को "कलन का मूलभूत प्रमेय" कहा जाता है।
- जहाँ
- जहाँ
सीमा योग के रूप में निश्चित समाकलन
जैसा कि पिछले अनुभाग में बताया गया है, हम दो दी गई सीमाओं के बीच एक वक्र के नीचे के क्षेत्र को अनंत संख्या में आयतों के योग के रूप में व्यक्त कर सकते हैं। इस अवधारणा का उपयोग करते हुए, एक निश्चित समाकल का मूल्यांकन करने के लिए, हम को अनंत संख्या में उपअंतरालों में विभाजित करके वक्र के नीचे के क्षेत्र को कई आयतों में विभाजित करते हैं। इस प्रकार, सीमा योग के रूप में निश्चित समाकल का सूत्र है:
यहाँ प्रत्येक उपअंतराल की लंबाई है।
FTC (फंडामेंटल थ्योरम ऑफ़ कैलकुलस) का उपयोग करके निश्चित समाकलन सूत्र
एक निश्चित समाकलन का मूल्यांकन कलन के मूलभूत प्रमेय (FTC) का उपयोग करके किया जा सकता है। यह एक निश्चित समाकलन का मूल्यांकन करने का सबसे आसान तरीका है। यह सूत्र कहता है कि सबसे पहले का प्रतिअवकलज (अनिश्चित समाकलन) ज्ञात करें (और इसे से निरूपित करें), पहले ऊपरी सीमा को प्रतिस्थापित करें और फिर एक-एक करके निचली सीमा को प्रतिस्थापित करें, और परिणामों को क्रम से घटाएँ। यानी,
जहाँ
निश्चित समाकलन की गणना
जैसा कि हमने पिछले अनुभाग में सीखा है, हम निश्चित समाकल की गणना दो तरीकों से कर सकते हैं: सीमा योग के रूप में व्याख्या करके और कलन के मूलभूत प्रमेय का उपयोग करके। हम इनमें से प्रत्येक सूत्र का उपयोग करके निश्चित समाकल का मूल्यांकन करेंगे और देखेंगे कि क्या हमें एक ही उत्तर मिलता है।