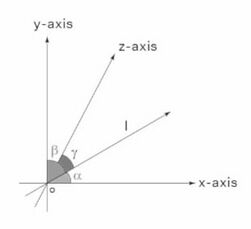
दिक्- कोसाइन, त्रि-आयामी अंतरिक्ष में रेखा द्वारा क्रमशः  -अक्ष,
-अक्ष,  -अक्ष,
-अक्ष,  -अक्ष के साथ बनाए गए कोण का कोसाइन है। दिक्- कोसाइन की गणना त्रि-आयामी अंतरिक्ष में एक सदिश या एक सरल रेखा के लिए की जा सकती है। यह त्रि- अक्षों के साथ रेखा द्वारा बनाए गए कोण का कोसाइन है।
-अक्ष के साथ बनाए गए कोण का कोसाइन है। दिक्- कोसाइन की गणना त्रि-आयामी अंतरिक्ष में एक सदिश या एक सरल रेखा के लिए की जा सकती है। यह त्रि- अक्षों के साथ रेखा द्वारा बनाए गए कोण का कोसाइन है।
आइए दिक्- कोसाइन, दिक्- कोसाइन के बीच संबंध और त्रि-आयामी अंतरिक्ष में दो बिंदुओं को जोड़ने वाली रेखा के दिक्- कोसाइन के बारे में अधिक जानें।
परिभाषा
दिक्- कोसाइन त्रि- आयामी अंतरिक्ष में एक सदिश या रेखा का संबंध त्रि- अक्षों में से प्रत्येक के साथ देता है। दिक्- कोसाइन इस रेखा द्वारा क्रमशः  -अक्ष,
-अक्ष,  -अक्ष और
-अक्ष और  -अक्ष के साथ अंतरित कोण का कोसाइन है। यदि रेखा द्वारा तीनों अक्षों के साथ अंतरित कोण
-अक्ष के साथ अंतरित कोण का कोसाइन है। यदि रेखा द्वारा तीनों अक्षों के साथ अंतरित कोण  ,
,  और
और  हैं, तो दिक्- कोसाइन क्रमशः
हैं, तो दिक्- कोसाइन क्रमशः  हैं।
हैं।
एक सदिश  के लिए दिक्- कोसाइन
के लिए दिक्- कोसाइन 
हैं।
दिक्- कोसाइन को  द्वारा भी दर्शाया जाता है और हम प्रायः दिक्- कोसाइन को इस प्रकार दर्शाते हैं
द्वारा भी दर्शाया जाता है और हम प्रायः दिक्- कोसाइन को इस प्रकार दर्शाते हैं  l त्रि-आयामी अंतरिक्ष में एक बिंदु
l त्रि-आयामी अंतरिक्ष में एक बिंदु  के लिए दिक्- कोसाइन इस बिंदु को मूल
के लिए दिक्- कोसाइन इस बिंदु को मूल  से जोड़ने वाली रेखा की दिक्- कोसाइन है। रेखा
से जोड़ने वाली रेखा की दिक्- कोसाइन है। रेखा  की दिक्- कोसाइन है l
की दिक्- कोसाइन है l 
दिक्- कोसाइन के बीच संबंध
बिंदु  को मूल बिंदु से जोड़ने वाली रेखा की दिक्- कोसाइन क्रमशः
को मूल बिंदु से जोड़ने वाली रेखा की दिक्- कोसाइन क्रमशः  है, और मूल बिंदु से इस बिंदु की दूरी
है, और मूल बिंदु से इस बिंदु की दूरी  है। यहाँ इन दिक्- कोसाइन के मान
है। यहाँ इन दिक्- कोसाइन के मान  . हैं दूरी
. हैं दूरी  का मान
का मान  है
है
यहाँ हमारा उद्देश्य इस बिंदु की दिक्- कोसाइन के बीच संबंध ज्ञात करना है। आइए हम बिंदु की दिक्- कोसाइन का वर्ग करें और उन्हें जोड़ें।


लेकिन हमारे पास  है। इसे उपरोक्त अभिव्यक्ति में प्रतिस्थापित करने पर हमें यह प्राप्त होता है।
है। इसे उपरोक्त अभिव्यक्ति में प्रतिस्थापित करने पर हमें यह प्राप्त होता है।


आइए अब हम  पर विचार करें। इसलिए हमारे पास दिक्- कोसाइन के बीच संबंध
पर विचार करें। इसलिए हमारे पास दिक्- कोसाइन के बीच संबंध  है।
है।
त्रि-आयामी ज्यामिति में दिक्- कोसाइन
दो बिंदुओं  और
और  को मिलाने वाली रेखा की दिक्- कोसाइन की गणना इन दो बिंदुओं को मिलाने वाली रेखाओं के दिक्- अनुपातों का उपयोग करके और इन दो बिंदुओं के बीच की दूरी ज्ञात करके आसानी से की जा सकती है। इन दो बिंदुओं को मिलाने वाली रेखा का दिक्- अनुपात
को मिलाने वाली रेखा की दिक्- कोसाइन की गणना इन दो बिंदुओं को मिलाने वाली रेखाओं के दिक्- अनुपातों का उपयोग करके और इन दो बिंदुओं के बीच की दूरी ज्ञात करके आसानी से की जा सकती है। इन दो बिंदुओं को मिलाने वाली रेखा का दिक्- अनुपात  है। और इन दो बिंदुओं के बीच की दूरी
है। और इन दो बिंदुओं के बीच की दूरी  है।
है।
किसी रेखा की दिक्- कोसाइन की गणना दो बिंदुओं के बीच की दूरी के साथ संबंधित दिक्- अनुपातों को विभाजित करके की जाती है। दो बिंदुओं को जोड़ने वाली रेखा के लिए दिक्- कोसाइन का सूत्र इस प्रकार है।
दिक्-कोसाइन 
उदाहरण
उदाहरण : बिंदु  को मूल बिंदु से मिलाने वाली रेखा की दिक्- कोसाइन ज्ञात करें।
को मूल बिंदु से मिलाने वाली रेखा की दिक्- कोसाइन ज्ञात करें।
समाधान:
मूल बिंदु  और बिंदु
और बिंदु  को मिलाने वाली रेखा के लिए दिक्- अनुपात
को मिलाने वाली रेखा के लिए दिक्- अनुपात  हैं।
हैं।
रेखा का परिमाण 
इसलिए दिक्- कोसाइन  हैं।
हैं।
इसलिए दिक्- कोसाइन  हैं।
हैं।