कोणों के युग्म

When angles appear in groups of two to display a certain geometrical property they are termed as pairs of angles. There is a special relationship between pairs of angles. Some of the angle pairs include complementary angles, supplementary angles, vertical angles, alternate interior angles, alternate exterior angles, corresponding angles, adjacent angles.

Linear Pair of Angles

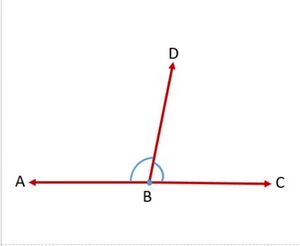
When two lines intersect each other, the adjacent angles make a linear pair. The sum of linear pairs is $180^{\circ }$. It should be noted that all linear pairs are supplementary because supplementary angles sum up to $180^{\circ }$. However, all supplementary angles need not be linear pairs because in linear pairs the lines need to intersect each other to form adjacent angles. In the following figure, $\angle ABD$ and $\angle CBD$ form a linear pair and their sum is equal to $180^{\circ }$. $\angle ABD+\angle CBD=180^{\circ }$

Fig. 1 - Linear Pair of angles

Linear Pair Axiom

Axiom 1: If a ray stands on a line, then the sum of two adjacent angles so formed is $180^{\circ }$.

Axiom 2: If the sum of two adjacent angles is $180^{\circ }$, then the non-common arms of the angles form a line.

In Fig.1 $BD$ is the common arm , $AB$ and $BC$ are the non-common arms.

Theorem 1

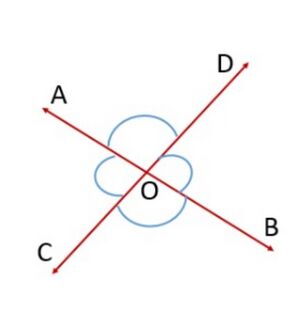
If two lines intersect each other, then the vertically opposite angles are equal.

Fig 2 - Vertically opposite angles

Proof : In the statement above, it is given that ‘two lines intersect each other’. So, let $AB$ and $CD$ be two lines intersecting at $O$ as shown in Fig. 2. They lead to two pairs of vertically opposite angles, namely, (i) $\angle AOC$ and $\angle BOD$ (ii) $\angle AOD$ and $\angle BOC$. We need to prove that $\angle AOC=\angle BOD$ and $\angle AOD=\angle BOC$

Now, ray $OA$ stands on line $CD$.

Hence $\angle AOC+\angle AOD=180^{\circ }......(1)$

ray $OD$ stands on line $AB$.

Hence $\angle AOD+\angle BOD=180^{\circ }......(2)$

From (1) and (2)

$\angle AOC+\angle AOD=\angle AOD+\angle BOD$

$\angle AOC=\angle BOD$

$OC$ stands on line $AB$.

Hence $\angle AOC+\angle BOC=180^{\circ }......(3)$

From (1) and (3)

$\angle AOC+\angle AOD=\angle AOC+\angle BOC$

$\angle AOD=\angle BOC$