कोणों के युग्म
जब कोण किसी निश्चित ज्यामितीय गुण को प्रदर्शित करने के लिए दो के समूह में दिखाई देते हैं तो उन्हें कोण युग्म कहा जाता है।कोण युग्मों के बीच एक विशेष संबंध होता है। कुछ कोण युग्मों में पूरक कोण, संपूरक कोण, ऊर्ध्वाधर कोण, वैकल्पिक आंतरिक कोण, वैकल्पिक बाह्य कोण, संगत कोण और आसन्न कोण उपस्थित हैं।
कोणों का रैखिक युग्म
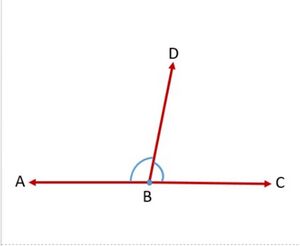
जब दो रेखाएँ एक दूसरे को प्रतिच्छेदहैं, तो आसन्न कोण एक रैखिक युग्म बनाते हैं। रैखिक युग्मों का योग होता है। यह ध्यान दिया जाना चाहिए कि सभी रैखिक युग्म संपूरक होते हैं क्योंकि संपूरक कोणों का योग होता है। हालाँकि, सभी संपूरक कोणों का रैखिक युग्म होना आवश्यक नहीं है क्योंकि रैखिक युग्मों में आसन्न कोण बनाने के लिए रेखाओं को एक दूसरे को प्रतिच्छेद आवश्यक होता है। निम्नलिखित चित्र में, कोण और कोण एक रैखिक युग्म बनाते हैं और उनका योग के समान होता है।
रैखिक युग्म अभिगृहीत
अभिगृहीत 1: यदि एक किरण किसी एक रेखा पर खड़ी हो, तो इस प्रकार बने दो आसन्न कोणों का योग होता है। .
अभिगृहीत 2: यदि दो आसन्न कोणों का योग है, तो कोणों की गैर-उभयनिष्ठ भुजाएँ एक रेखा बनाती हैं।
चित्र 1 में सम्भ्य भुजा है, और गैर-उभयनिष्ठ भुजाएँ हैं।
प्रमेय 1
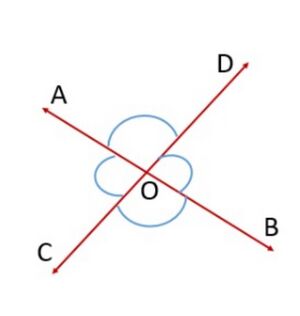
यदि दो रेखाएँ एक दूसरे को प्रतिच्छेद करती हैं, तो ऊर्ध्वाधर विपरीत कोण समान होते हैं।
प्रमाण: उपरोक्त कथन में, यह दिया गया है कि 'दो रेखाएँ एक दूसरे को प्रतिच्छेद करती हैं'। इसलिए, मान लीजिए कि और दो रेखाएँ हैं जो पर प्रतिच्छेद करती हैं जैसा कि चित्र-2 में दिखाया गया है। वे ऊर्ध्वाधर रूप से विपरीत कोणों के दो युग्म बनाते हैं, अर्थात्, (i) और (ii) और ।हमें यह सत्यापन करना होगा कि और
अब किरण , रेखा पर खडी है।
अत:
किरण, रेखा पर खडी है।
अत:
(1) एवं (2)) से
, रेखा पर खडी है।
अत:
(1) एवं (3) से