कोणों के युग्म: Difference between revisions
(added content) |
(added content) |
||
| Line 2: | Line 2: | ||
== कोणों का रैखिक युग्म == | == कोणों का रैखिक युग्म == | ||
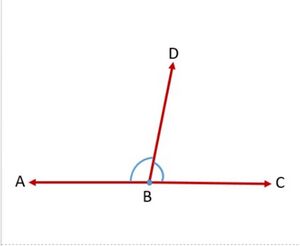
जब दो रेखाएँ एक दूसरे को काटती हैं, तो आसन्न कोण एक रैखिक युग्म बनाते हैं। रैखिक युग्मों का योग <math>180^\circ</math>होता है। यह ध्यान दिया जाना चाहिए कि सभी रैखिक युग्म संपूरक होते हैं क्योंकि संपूरक कोणों का योग <math>180^\circ</math>होता है। हालाँकि, सभी संपूरक कोणों का रैखिक युग्म होना आवश्यक नहीं है क्योंकि रैखिक युग्मों में आसन्न कोण बनाने के लिए रेखाओं को एक दूसरे को काटना आवश्यक होता है। निम्नलिखित चित्र में, <math>\angle ABD</math> कोण और <math>\angle CBD</math> कोण एक रैखिक युग्म बनाते हैं और उनका योग <math>180^\circ</math> के बराबर होता है। <math>\angle ABD+\angle CBD=180^\circ</math> | |||
[[File:Linear Pair of angles.jpg|alt=Fig. 1 - Linear Pair of angles|none|thumb|Fig. 1 - Linear Pair of angles]] | [[File:Linear Pair of angles.jpg|alt=Fig. 1 - Linear Pair of angles|none|thumb|Fig. 1 - Linear Pair of angles]] | ||
Revision as of 08:17, 27 June 2024
जब कोण किसी निश्चित ज्यामितीय गुण को प्रदर्शित करने के लिए दो के समूह में दिखाई देते हैं तो उन्हें कोण युग्म कहा जाता है।कोण युग्मों के बीच एक विशेष संबंध होता है। कुछ कोण युग्मों में पूरक कोण, संपूरक कोण, ऊर्ध्वाधर कोण, वैकल्पिक आंतरिक कोण, वैकल्पिक बाह्य कोण, संगत कोण और आसन्न कोण शामिल हैं।
कोणों का रैखिक युग्म
जब दो रेखाएँ एक दूसरे को काटती हैं, तो आसन्न कोण एक रैखिक युग्म बनाते हैं। रैखिक युग्मों का योग होता है। यह ध्यान दिया जाना चाहिए कि सभी रैखिक युग्म संपूरक होते हैं क्योंकि संपूरक कोणों का योग होता है। हालाँकि, सभी संपूरक कोणों का रैखिक युग्म होना आवश्यक नहीं है क्योंकि रैखिक युग्मों में आसन्न कोण बनाने के लिए रेखाओं को एक दूसरे को काटना आवश्यक होता है। निम्नलिखित चित्र में, कोण और कोण एक रैखिक युग्म बनाते हैं और उनका योग के बराबर होता है।
रैखिक युग्म अभिगृहीत
Axiom 1: If a ray stands on a line, then the sum of two adjacent angles so formed is .
Axiom 2: If the sum of two adjacent angles is , then the non-common arms of the angles form a line.
In Fig.1 is the common arm , and are the non-common arms.
Theorem 1
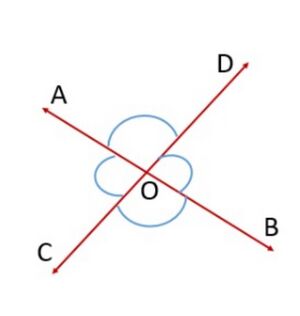
If two lines intersect each other, then the vertically opposite angles are equal.
Proof : In the statement above, it is given that ‘two lines intersect each other’. So, let and be two lines intersecting at as shown in Fig. 2. They lead to two pairs of vertically opposite angles, namely, (i) and (ii) and . We need to prove that and
Now, ray stands on line .
Hence
ray stands on line .
Hence
From (1) and (2)
stands on line .
Hence
From (1) and (3)