वास्तविक संख्याएँ: Difference between revisions

Latest revision as of 17:08, 16 October 2024

वास्तविक संख्याएँ

वास्तविक संख्याओं को परिमेय और अपरिमेय संख्याओं दोनों के संयोजन के रूप में परिभाषित किया जा सकता है। वे सकारात्मक और नकारात्मक दोनों हो सकते हैं। सभी प्राकृत संख्याएँ, दशमलव तथा भिन्न इस श्रेणी में आते हैं।

परिमेय संख्याएँ	${\frac {7}{3}}$ , 0.63
पूर्णांक	......-3 , -2 , -1 , 0 , 1 , 2 , 3 .........
पूर्ण संख्याएँ	0 , 1 , 2 , 3.......
प्राकृतिक संख्याएँ	1 , 2 , 3 ........

अपरिमेय संख्याएँ	${\sqrt {2}}$ , π , 0.10100110...

वास्तविक संख्याओं के गुणधर्म

वास्तविक संख्याओं के चार मुख्य गुण निम्नलिखित हैं:

क्रमचयी गुणधर्म
साहचर्य गुणधर्म
वितरणात्मक गुणधर्म
तत्समक गुणधर्म

मान लीजिए कि “ $m$ , $n$ और $r$ ” तीन वास्तविक संख्याएँ हैं। तब उपरोक्त गुणों का उपयोग करके वर्णन किया जा सकता है

जैसा कि नीचे दिखाया गया है $m$ , $n$ और $r$ :

क्रमचयी गुणधर्म

यदि $m$ और $n$ संख्याएँ हैं, तो योग के लिए $m+n=n+m$ और गुणन के लिए $m.n=n.m$ सामान्य रूप होगा ।

योग : $m+n=n+m$ . उदाहरण के लिए, $6+3=3+6,2+8=8+2$ .
गुणन : $m\times n=n\times m$ . उदाहरण के लिए, $6\times 3=3\times 6,2\times 8=8\times 2$ .

साहचर्य गुणधर्म यदि $m$ और $n$ संख्याएँ हैं । $m+(n+r)=(m+n)+r$ योग के लिए और $(mn)r=m(nr)$ गुणन के लिए, सामान्य रूप होगा ।

योग : $m+(n+r)=(m+n)+r$ सामान्य रूप होगा। योगात्मक साहचर्य गुणधर्म का एक उदाहरण $8+(3+2)=(8+3)+2$ है ।
गुणन : $(mn)r=m(nr)$ । $(2\times 6)5=2(6\times 5)$ गुणनात्मक साहचर्य गुणधर्म का एक उदाहरण है ।

वितरणात्मक गुणधर्म

तीन संख्याओं के लिए यदि $m$ , $n$ , और $r$ जो प्रकृति में वास्तविक हैं, तो वितरणात्मक गुण को इस प्रकार दर्शाया गया है:

$m(n+r)=mn+mr$ तथा $(m+n)r=mr+nr$

वितरणात्मक गुणधर्म का उदाहरण है: $5(2+3)=5\times 2+5\times 3$ । यहाँ, दोनों पक्षों से 25 प्राप्त होगा।

तत्समक गुणधर्म

योगात्मक और गुणात्मक सर्वसमिकाएँ होती हैं।

योग के लिए : $m+0=m$ . ( $0$ योगात्मक तत्समक है)
गुणन के लिए : $m\times 1=1\times m=m$ . ( $1$ गुणात्मक तत्समक है)

उदाहरण

निम्नलिखित में से वास्तविक संख्याएँ पहचानें: ${\sqrt {6}},-3,3.15,-{\frac {1}{2}},{\sqrt {-5}}$

हल: दी गई संख्याओं में से ${\sqrt {-5}}$ एक सम्मिश्र संख्या है। अत: यह वास्तविक संख्या नहीं हो सकती। अन्य संख्याएँ या तो परिमेय या अपरिमेय हैं। इस प्रकार, वे वास्तविक संख्याएँ हैं। इसलिए, सूची से ${\sqrt {6}},-3,3.15,-{\frac {1}{2}}$ वास्तविक संख्याएँ हैं

@@ Line 1: / Line 1: @@
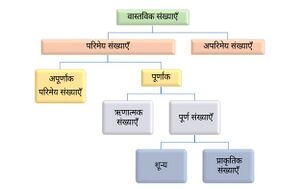
+[[File:Real-Numbers (Hindi).jpg|thumb|वास्तविक संख्याएँ]]
-वास्तविक संख्याओं को परिमेय और अपरिमेय संख्याओं दोनों के संयोजन के रूप में परिभाषित किया जा सकता है। वे सकारात्मक और नकारात्मक दोनों हो सकते हैं। सभी प्राकृत संख्याएँ, दशमलव तथा भिन्न इस श्रेणी में आते हैं।
+वास्तविक संख्याओं को [[परिमेय संख्याएँ|परिमेय]] और [[अपरिमेय संख्याएँ|अपरिमेय]] संख्याओं दोनों के संयोजन के रूप में परिभाषित किया जा सकता है। वे सकारात्मक और नकारात्मक दोनों हो सकते हैं। सभी प्राकृत संख्याएँ, दशमलव तथा भिन्न इस श्रेणी में आते हैं।
 {| class="wikitable"
 |[[परिमेय संख्याएँ]]
@@ Line 18: / Line 18: @@
 |<math>\sqrt{2}</math>  ,  π ,  0.10100110...
 |}
-[[Category:संख्या पद्धति]][[Category:कक्षा-9]][[Category:गणित]][[Category:गणित]]
+== वास्तविक संख्याओं के गुणधर्म ==
+वास्तविक संख्याओं के चार मुख्य गुण निम्नलिखित हैं:
+* क्रमचयी गुणधर्म
+* साहचर्य गुणधर्म
+* वितरणात्मक गुणधर्म
+* तत्समक  गुणधर्म
+मान लीजिए कि “<math>m</math>,<math>n</math> और <math>r</math>” तीन वास्तविक संख्याएँ हैं। तब उपरोक्त गुणों का उपयोग करके वर्णन किया जा सकता है
+जैसा कि नीचे दिखाया गया है <math>m</math>,<math>n</math> और <math>r</math> :
+'''क्रमचयी गुणधर्म'''
+यदि <math>m</math> और <math>n</math> संख्याएँ हैं, तो योग के लिए  <math>m+n=n+m</math> और गुणन के लिए  <math>m.n=n.m</math>  सामान्य रूप होगा ।
+*'''योग :''' <math>m+n=n+m</math>. उदाहरण के लिए, <math>6+3=3+6 , 2+8=8+2</math>.
+*'''गुणन :''' <math>m \times n=n \times m</math>. उदाहरण के लिए, <math>6 \times 3=3 \times 6, 2 \times 8=8 \times 2</math>.
+'''साहचर्य गुणधर्म'''
+यदि <math>m</math> और <math>n</math> संख्याएँ हैं । <math>m +(n+r)=(m+n)+r</math>  योग के लिए और <math>(mn)r=m(nr)</math> गुणन के लिए, सामान्य रूप होगा ।
+*'''योग :''' <math>m +(n+r)=(m+n)+r</math> सामान्य रूप होगा। योगात्मक साहचर्य गुणधर्म का एक उदाहरण <math>8 +(3+2)=(8+3)+2</math> है ।
+*'''गुणन :''' <math>(mn)r=m(nr)</math>। <math>(2 \times 6)5=2(6 \times 5)</math>गुणनात्मक साहचर्य गुणधर्म का एक उदाहरण है ।
+'''वितरणात्मक गुणधर्म'''
+तीन संख्याओं के लिए यदि <math>m</math>,<math>n</math>, और <math>r</math> जो प्रकृति में वास्तविक हैं, तो वितरणात्मक गुण को इस प्रकार दर्शाया गया है:
+<math>m(n+r)=mn+mr</math> तथा <math>(m+n)r=mr+nr</math>
+* वितरणात्मक गुणधर्म का उदाहरण है: <math>5(2+3)=5 \times 2 + 5 \times 3</math>। यहाँ, दोनों पक्षों से 25 प्राप्त होगा।
+'''तत्समक  गुणधर्म'''
+योगात्मक और गुणात्मक सर्वसमिकाएँ होती हैं।
+*'''योग''' '''के लिए :''' <math>m+0=m</math>. (<math>0</math> योगात्मक तत्समक है)
+*'''गुणन के लिए :''' <math>m \times 1= 1 \times m =m</math>. (<math>1</math> गुणात्मक तत्समक है)
+== उदाहरण ==
+निम्नलिखित में से वास्तविक संख्याएँ पहचानें:  <math>\sqrt 6,-3,3.15,-\frac{1}{2},\sqrt{-5}</math>
+हल: दी गई संख्याओं में से <math>\sqrt{-5}</math> एक सम्मिश्र संख्या है। अत: यह वास्तविक संख्या नहीं हो सकती। अन्य संख्याएँ या तो परिमेय या अपरिमेय हैं। इस प्रकार, वे वास्तविक संख्याएँ हैं। इसलिए, सूची से <math>\sqrt 6,-3,3.15,-\frac{1}{2}</math> वास्तविक संख्याएँ हैं
+[[Category:संख्या पद्धति]]
+[[Category:गणित]]
+[[Category:कक्षा-9]][[Category:गणित]]