एक ही रेखा के समानांतर रेखाएँ: Difference between revisions
(added content) |
(added internal links) |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
हम जानते हैं कि रेखा <math>m || </math> रेखा <math>l </math> और रेखा <math>n || </math> रेखा <math>l </math> है। | हम जानते हैं कि रेखा <math>m || </math> रेखा <math>l </math> और रेखा <math>n || </math> रेखा <math>l </math> है। | ||
अतः <math>\angle 1=\angle 2 </math> और <math>\angle 1=\angle 3 </math> (संगत [[कोण]] अभिगृहीत) | |||
परंतु <math>\angle 2=\angle 3 </math> क्योंकि वे संगत कोण हैं | |||
अतः, हम कह सकते हैं कि रेखा <math>m || </math> रेखा <math>n </math> (संगत कोण अभिगृहीत का विलोम) | |||
इस परिणाम को निम्नलिखित प्रमेय के रूप में बताया जा सकता है: | |||
''' | '''प्रमेय 1:''' वे रेखाएँ जो एक ही रेखा के समानान्तर होती हैं, एक दूसरे के समानान्तर होती हैं। | ||
== उदाहरण == | |||
दिए गए चित्र से, <math>AB ||CD </math>, <math>CD ||EF </math>, <math>EA \perp AB </math> और <math>\angle BEF =55^\circ </math>। <math>x,y,z </math>. का मान ज्ञात कीजिए। | |||
[[File:Lines parallel to the same line - 1.jpg|alt=Fig. 2|none|thumb|चित्र. 2]] | |||
'''हल:''' | |||
[[ | मान लें कि <math>AB ||CD </math>, <math>CD ||EF </math>, <math>EA \perp AB </math> और <math>\angle BEF =55^\circ </math> | ||
अतः, <math>y + 55^\circ =180^\circ </math> (अनुप्रस्थ रेखा <math>ED </math> के एक ही तरफ आंतरिक कोण ) | |||
इसलिए, <math>y =180^\circ -55^\circ =125^\circ </math> | |||
संगत कोण [[अभिगृहीत]] का उपयोग करके, <math>AB ||CD </math>, हम ऐसा कह सकते हैं <math>x=y </math>। | |||
अतः, <math>x =125^\circ </math> का मूल्य | |||
चूँकि, <math>AB ||CD </math> और <math>CD ||EF </math>, इसलिए <math>AB ||EF </math>। | |||
इसलिए, हम लिख सकते हैं: <math>\angle FEA + \angle EAB=180^\circ </math>(अनुप्रस्थ रेखा <math>EA </math> के एक ही तरफ आंतरिक कोण ) | |||
<math>55^\circ+z+90^\circ=180^\circ </math> | |||
<math>z=180^\circ-90^\circ-55^\circ = 35^\circ </math> | |||
इसलिए, <math>x,y,z </math> के मान <math>125^\circ,125^\circ,35^\circ </math> क्रमशः हैं। | |||
[[Category:कक्षा-9]][[Category:गणित]] | |||
[[Category:रेखाएँ और कोण]] | |||
Latest revision as of 08:26, 5 November 2024
यदि दो रेखाएँ एक ही रेखा के समानान्तर हों तो क्या वे एक-दूसरे के समानान्तर होंगी? आइए सत्यापित करें।
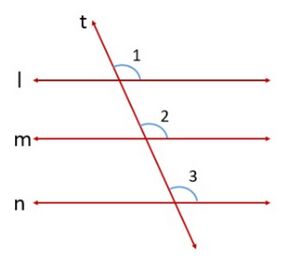
चित्र-1 में रेखा रेखा और रेखा रेखा ।
आइए हम रेखाओं के लिए एक रेखा अनुप्रस्थ रेखा खींचें
हम जानते हैं कि रेखा रेखा और रेखा रेखा है।
अतः और (संगत कोण अभिगृहीत)
परंतु क्योंकि वे संगत कोण हैं
अतः, हम कह सकते हैं कि रेखा रेखा (संगत कोण अभिगृहीत का विलोम)
इस परिणाम को निम्नलिखित प्रमेय के रूप में बताया जा सकता है:
प्रमेय 1: वे रेखाएँ जो एक ही रेखा के समानान्तर होती हैं, एक दूसरे के समानान्तर होती हैं।
उदाहरण
दिए गए चित्र से, , , और । . का मान ज्ञात कीजिए।
हल:
मान लें कि , , और
अतः, (अनुप्रस्थ रेखा के एक ही तरफ आंतरिक कोण )
इसलिए,
संगत कोण अभिगृहीत का उपयोग करके, , हम ऐसा कह सकते हैं ।
अतः, का मूल्य
चूँकि, और , इसलिए ।
इसलिए, हम लिख सकते हैं: (अनुप्रस्थ रेखा के एक ही तरफ आंतरिक कोण )
इसलिए, के मान क्रमशः हैं।